DETERMINANTS

We know that not every system of linear equations has a single solution. Sometimes a system of n equations in n variables has no solution or an infinite set of solutions. In this section, we introduce the determinant of a matrix. We shall see in in a subsequent sectionthat the determinant can be used to determine whether a system of equations has a single solution.

 Every square matrix A is associated with a real number called the determinant of A, written |A|.

The determinant of a 2 x 2 matrix A,

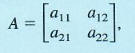
is defined as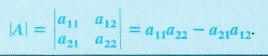




NOTE Notice that matrices are enclosed with square brackets, while determinants are denoted with vertical bars. Also, the matrix is an array of numbers, but its determinant is a single number.

EVALUATING A 2 X 2 DETERMINANT

If

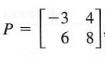
then

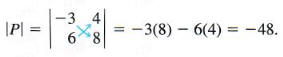
DETERMINANT OF A 3 X 3 MATRIX

The determinant of a 3 x 3 matrix A,

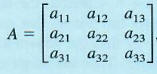
is defined as

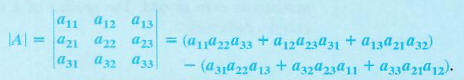
An easy method for calculating 3 X 3 determinants is found by rearranging and factoring the terms given above to get

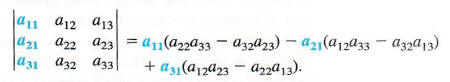
Each of the quantities in parentheses represents the determinant of a 2 X 2 matrix that is the part of the 3 x 3 matrix remaining when the row and column of the multiplier are eliminated, as shown below.

These determinants of the 2 X 2 matrices are called minors of an element in the 3 x 3 matrix. The symbol M_ij represents the determinant of the matrix that results when row i and column j are eliminated. The following list gives some of the minors from the matrix above.

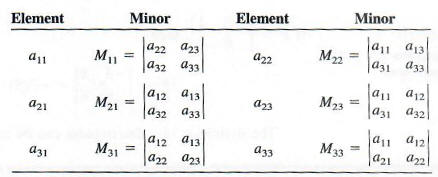
In a 4 x 4 matrix, the minors are determinants of 3 X 3 matrices, and an n x n matrix has minors that are determinants of (n - 1) X (n - 1) matrices.
To find the determinant of a 3 X 3 or larger matrix, first choose any row or column. Then the minor of each element in that row or column must be multiplied by + l or - 1, depending on whether the sum of the row numbers and column numbers is even or odd. The product of a minor and the number + 1 or - l is called a cofactor.

COFACTOR Let M_ij be the minor for element au in an n x n matrix. The cofactor of a_ij, written A_ij, is:

Finally, the determinant of an n x n matrix is found as follows.

FINDING THE DETERMINANT OF' A MATRIX
Multiply each element in any row or column of the matrix by its cofactor. The sum of these products gives the value of the determinant.The process of forming this sum of products is called expansion by a given row or column.


FINDING THE COFACTOR OF AN ELEMENT
For the matrix

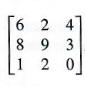
find the cofactor of each of the following elements.

(a) 6
Since 6 is in the first row and first column of the matrix, i = 1 and j = 1.

The cofactor is (-1)¹⁺¹ * (-6) = 1 * (-6) = -6.

(b) 3
Here i = 2 and j = 3.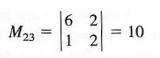


The cofactor is (-1)²⁺³ * 10 = (-1) * 10 = -10.

(c) 8
We have i = 2 and j = l.

The cofactor is (-1)²⁺¹ * (-8) = (-1) * (-8) = 8.

 

EVALUATING A 3 X 3 DETERMINANT
Evaluate

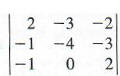
expanding by the second column.

To find this determinant, first get the minors of each element in the second column.

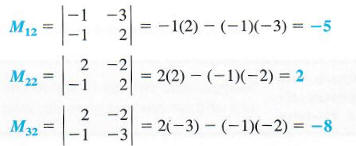
Now find the cofactor of each of these minors.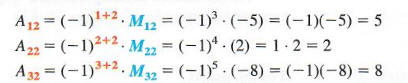

The determinant is found by multiplying each cofactor by its corresponding element in the matrix and finding the sum of these products.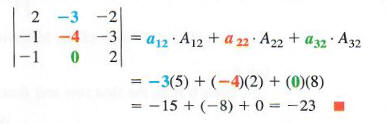

CAUTION: Be very careful to keep track of all negative signs when evaluating determinants. Work carefully, writing down each step as in the examples. Skipping steps frequently leads to errors in these computations.

Exactly the same answer would be found using any row or column of the ma trix. One reason that column 2 was used in Example 3 is that it contains a 0 element, so that it was not really necessary to calculate M₃₂ and A₃₂ above. One learns quickly that zeros can be very useful in working with determinants.
Instead of calculating (-1)^i+j for a given element, the following sign checker boards can be used:

The signs alternate for each row and column, beginning with + in the first row, first column position. Thus, these arrays of signs can be reproduced as needed. If we expand a 3 X 3 matrix about row 3, for example, the first minor would have a + sign associated with it, the second minor a - sign, and the third minor a + sign. These arrays of signs can be extended in this way for determinants of 5 X 5, 6 X 6, and larger matrices.

EVALUATING A 4 X 4 DETERMINANT
Evaluate


Expanding by minors about the fourth row gives

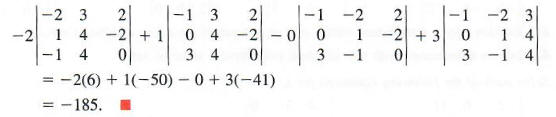
Each of the four determinants in Example 4 must be evaluated by expansion of three minors, requiring much work to get the final value. Always look for the row or column with the most zeros to simplify the work. In the next section we introduce several properties that make it easier to calculate determinants. Fortunately, determinants of large matrices can be evaluated quickly and easily with the aid of a computer or with certain calculators.