Expanding Polynomials

MONOMIALS MULTIPLIED BY POLYNOMIALS

OBJECTIVES

Upon completing this section you should be able to:

Recognize polynomials.
Identify binomials and trinomials.
Find the product of a monomial and binomial.

A polynomial is the sum or difference of one or more monomials.

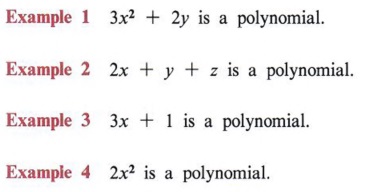
Generally, if there is more than one variable, a polynomial is written in alphabetical order.

Special names are used for some polynomials. If a polynomial has two terms it is called a binomial.

If a polynomial has three terms it is called a trinomial.

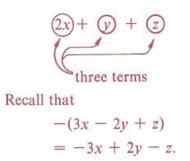
In the process of removing parentheses we have already noted that all terms in the parentheses are affected by the sign or number preceding the parentheses. We now extend this idea to multiply a monomial by a polynomial.

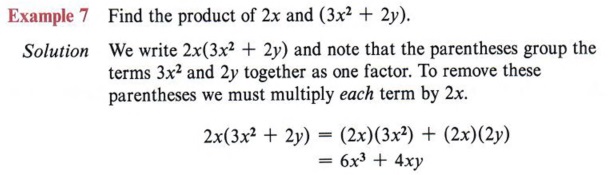
Placing 2x directly in front of the parentheses means to multiply the expression in the parentheses by 2x. Notice each term is multiplied by 2x.

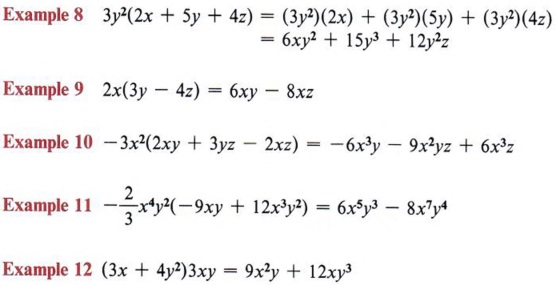
Again, each term in the parentheses is multiplied by 3y²

Again, each term in the parentheses is multiplied by 3y².
In each of these examples we are using the distributive property.

PRODUCTS OF POLYNOMIALS

OBJECTIVES

Upon completing this section you should be able to:

Find the product of two binomials.
Use the distributive property to multiply any two polynomials.

In the previous section you learned that the product A(2x + y) expands to A(2x) + A(y).

Now consider the product (3x + z)(2x + y).

Since (3x + z) is in parentheses, we can treat it as a single factor and expand (3x + z)(2x + y) in the same manner as A(2x + y). This gives us

If we now expand each of these terms, we have

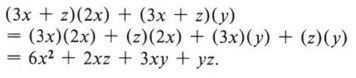
Notice that in the final answer each term of one parentheses is multiplied by every term of the other parentheses.

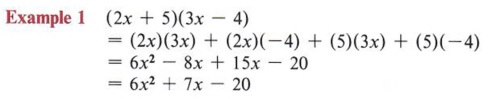
Note that this is an application of the distributive property.

Since - 8x and 15x are similar terms, we may combine them to obtain 7x.

In this example we were able to combine two of the terms to simplify the final answer.

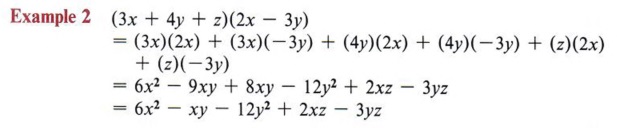
Here again we combined some terms to simplify the final answer. Note that the order of terms in the final answer does not affect the correctness of the solution.

The commutative property allows the rearrangement of order.

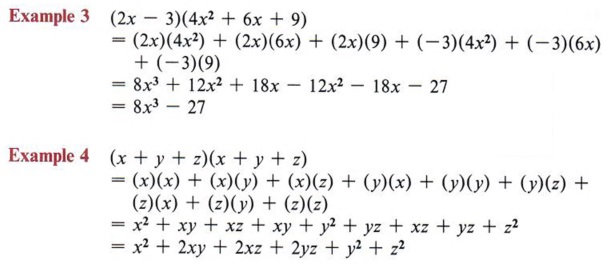
Try to establish a system for multiplying each term of one parentheses by each term of the other. In these examples we have taken the first term in the first set of parentheses and multiplied it by each term in the second set of parentheses. Then we took the second term of the first set and multiplied it by each term of the second set, and so on.