Equations
The equations section of QuickMath allows you to solve and plot virtually any equation or system of equations. In most cases, you can find exact solutions to your equations. Even when this is not possible, QuickMath may be able to give you approximate solutions to almost any level of accuracy you require. It also contains a number of special commands for dealing with quadratic equations.
Solve
The Solve command can be uses to solve either a single equation for a single unknown from the basic solve page or to simultaneously solve a system of many equations in many unknowns from the advanced solve page. The advanced command allows you to specify whether you want approximate numerical answers as well as exact ones, and how many digits of accuracy (up to 16) you require. It also allows you to eliminate certain variables from the equations.
Plot
The Plot command, from the Graphs section, will plot any function of two variables. In order to plot a single function of x, go to the basic equation plotting page, where you can enter the equation and specify the upper and lower limits on x that you want the graph to be plotted for. The advanced plotting page allows you to plot up to 6 equations on the one graph, each with their own color. It also gives you control over such things as whether or not to show the axes, where the axes should be located, what the aspect ratio of the plot should be and what the range of the dependent variable should be. All equations can be given in the explicit y = f(x) form or the implicit g(x,y) = c form.
Go to the Equation Plotting page
Quadratics
The Quadratics page contains 13 separate commands for dealing with the most common questions concerning quadratics. It allows you to : factor a quadratic function (by two different methods); solve a quadratic equation by factoring the quadratic, using the quadratic formula or by completing the square; rewrite a quadratic function in a different form by completing the square; calculate the concavity, x-intercepts, y-intercept, axis of symmetry and vertex of a parabola; plot a parabola; calculate the discriminant of a quadratic equation and use the discriminant to find the number of roots of a quadratic equation. Each command generates a complete and detailed custom-made explanation of all the steps needed to solve the problem.
Introduction to Equations
By an equation we mean a mathematical sentence that states that two algebraic expressions are equal. For example, a (b + c) =ab + ac, ab = ba, and x2-1 = (x-1)(x+1) are all equations that we have been using. We recall that we defined a variable as a letter that may be replaced by numbers out of a given set, during a given discussion. This specified set of numbers is sometimes called the replacement set. In this chapter we will deal with equations involving variables where the replacement set, unless otherwise specified, is the set of all real numbers for which all the expressions in the equation are defined.
If an equation is true after the variable has been replaced by a specific number, then the number is called a solution of the equation and is said to satisfy it. Obviously, every solution is a member of the replacement set. The real number 3 is a solution of the equation 2x-1 = x+2, since 2*3-1=3+2. while 1 is a solution of the equation (x-1)(x+2) = 0. The set of all solutions of an equation is called the solution set of the equation.
In the first equation above {3} is the solution set, while in the second example {-2,1} is the solution set. We can verify by substitution that each of these numbers is a solution of its respective equation, and we will see later that these are the only solutions.
A conditional equation is an equation that is satisfied by some numbers from its replacement set and not satisfied by others. An identity is an equation that is satisfied by all numbers from its replacement set.
Example 1 Consider the equation 2x-1 = x+2
The replacement set here is the set of all real numbers. The equation is conditional since, for example, 1 is a member of the replacement set but not of the solution set.
Example 2 Consider the equation (x-1)(x+1) =x2-1
The replacement set is the set of all real numbers. From our laws of real
numbers if a is any real number, then (a-1)(a+1) = a2 -1
Therefore, every member of the replacement set is also a member of the solution
set. Consequently this equation is an identity.
Example 3 Consider
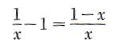
The replacement set for this equation is the set of real numbers except 0, since 1/x and (1- x)/x are not defined for x = 0. If a is any real number in the replacement set, then
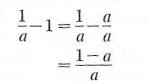
so that the original equation is an identity.
Example 4 Consider
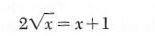
The replacement set is the set of all non-negative real numbers, since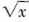 is not a real number if x is negative. The equation is conditional since, for example, 4 is a member of the replacement set but not of the solution
set.
is not a real number if x is negative. The equation is conditional since, for example, 4 is a member of the replacement set but not of the solution
set.