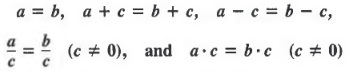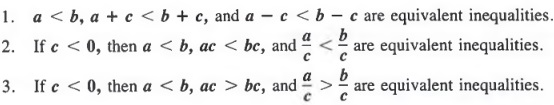INEQUALITIES IN ONE VARIABLE

ORDER RELATIONSHIPS

In Sections 1.1 and 2.1, we saw that of two different numbers, the graph of the lesser number lies to the left of the graph of the greater number on a number line. These order relationships can be expressed by using the following symbols:

< means "is less than,"

> means "is greater than."

≤ means "is less than or equal to,"

≥ means "is greater than or equal to."

For example,

"1 is less than 3" can be written as 1 < 3.

"7 is less than 9" can be written as 7 < 9.

"-3 is greater than -5" can be written as -3 > -5.

"2 is less than or equal to x" can be written as 2 ≤ x.

"4 is greater than or equal to y" can be written as 4 ≥ y.

Statements that involve any of the above symbols are called inequalities. Inequalities such as

1 < 3 and 7 < 9

are said to be of the same order or same sense because the left-hand member is less than the right-hand member in each case. Inequalities such as

7 < 9 and -3 > -5

are said to be of opposite order or opposite sense because in one case the left-hand member is less than the right-hand member and in the other case the left-hand member is greater than the right-hand member.

PROPERTIES OF INEQUALITIES

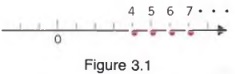
In Section 3.1, we saw that a first-degree equation in one variable has only one solution. But a first-degree inequality has an infinite number of solutions. For example, the graphs of the infinite number of integer solutions of the inequality x > 3 are shown in Figure 3.1.

Sometimes it is not possible to determine the solutions of a given inequality simply by inspection. But using the following properties, we can form equivalent inequalities (inequalities with the same solutions) in which the solution is evident by inspection.

1. If the same expression is added to or subtracted from each member of an inequality, the result is an equivalent inequality in the same order.

In symbols,

a < b, a + c < b + c, and a - c < b - c

are equivalent inequalities.

Example 1 a. Because 3 < 5, then

3 + 4 < 5 + 4 or 7<9

b. If x < 7, then

x + 2 < 7 + 2

c. If 4 < y, then

4 + (-2) < y + (-2)

2. If each member of an inequality is multiplied or divided by the same positive number, the result is an equivalent Inequality in the same order.

In symbols,

are equivalent inequalities.

Example 2 a. Because 2 < 3 and 5 > 0,

2(5) < 3(5) or 10 < 15

b. If 3x < 12, then

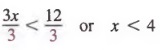
c. If 5 < y and z > 0, then

5(z) < y(z) or 5z < yz

3. If each member of an inequality is multiplied or divided by the same negative number, the result is an equivalent inequality in the opposite order.

In symbols,

are equivalent inequalities.

Example 3 a. Because 3 < 5 and -2 < 0,

3(-2) > 5( -2) or -6 >-10

b. If -3x < 12, then

c. If 2 < x and y < 0, then

2(y) > x(y) or 2y > xy

The three properties above also apply to inequalities of the form a > b, as well as a < b.

SOLVING INEQUALITIES

Now let us see how the three properties can help us solve inequalities.

Example 4 Solve , where x is an integer.

Solution Multiplying each member by 2 (a positive number), we have

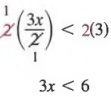
Then dividing each member by 3, we get

The graph of this inequality is

In the above example, all the inequalities were in the same order because we only applied Property 2 above. Now consider the following inequality.

Example 5 Solve - 3x + 1 > 7, where x is an integer.

Solution Adding - 1 to each member, we get

-3x + 1 + (-1) > 7 + (-1)

-3x > 6

Now we apply Property 3 and divide each member by -3. In this case we have to reverse the order of the inequality.

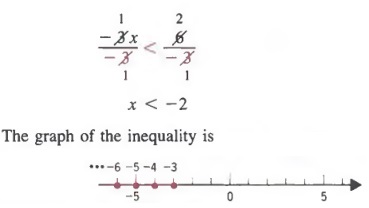
When solving word problems involving inequalities, we follow the six steps outlined on page 115 except the word equation will be replaced by the word inequality.

CHAPTER SUMMARY

1. Symbolic versions of word sentences are called equations. Equations in which the variable has an exponent of 1 are first-degree equations. A value of the variable for which an equation is true is called a solution of the equation.
2. Equations that have identical solutions are called equivalent equations. An equation whose solution is not evident by inspection can be transformed to an equivalent equation whose solution is evident. We do this by applying one or more of the following properties:
   
   
   are equivalent equations. By the symmetric property of equality, the members of an equation can be interchanged without any changes of sign. Thus,
   
   if a = b, then b = a
3. We can solve a folumula by substituting known values into the formula and solving for the unknown variable. We can also solve for a given variable in terms of the other variables.
4. We can use the following properties to write equivalent inequalities:
   
   
   We must reverse the inequality whenever we multiply or divide both members of an inequality by a negative number.

TRANSLATING WORD SENTENCES

Most problems that deal with practical applications of mathematics are expressed in words. Before we can solve such problems, we must translate word sentences into mathematical equations. We can then use the techniques of the previous sections to solve the equations.

In this section, we will only be concerned with writing algebraic expressions and equations. In the following sections, we will actually solve equations.

In Sections 1.2 and 1.3 we associated certain word phrases with certain mathematical operations:

1. "The sum of," "increased by," "plus," "more than," "add," "exceeds," and "exceeded by" can be associated with addition.
2. "Take away," "less than," "diminished by," "deducted from," "subtract," "subtracted from," "less," and "difference of" can be associated with subtraction.
3. "Times," "multiply," "twice (two times)," "of," and "product of" can be associated with multiplication.
4. "Divided by" and "quotient of" can be associated with division.

We can translate these word phrases into algebraic expressions as shown in the following examples.

Example 1

Similarly, we can translate word sentences into equations.

Example 2

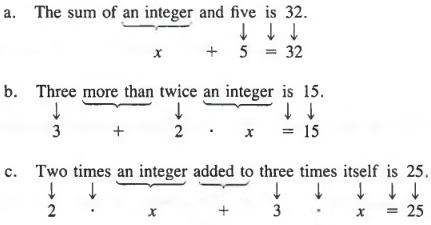
Common Errors: When translating a phrase such as "a subtracted from b," the order is important. We must write

b - a, not a - b

since a is subtracted from b. For example, to translate

"If seven is subtracted from 4 times an integer, the result is 17,"

we represent the integer by a symbol, say x, and then write the sentence as follows.

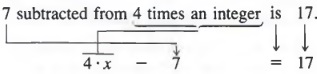
APPLICATIONS

In the last section we translated word sentences into equations. Now, we will solve a variety of word problems. The following steps are suggested.

To solve a word problem:

1. Represent each quantity you want to find as a word phrase.
2. Represent each quantity from step 1 in terms of a single variable.
3. When applicable, make a sketch or a table and indicate all quantities.
4. Write an equation that represents a word sentence relating the known and unknown quantities.
5. Solve the resulting equation.
6. Using the result from step 5, answer the original question.

In practice, we usually combine steps 1 and 2.

Follow the six steps listed above to solve the following word problem.

The sum of a certain number and 9 is equal to four times the number. What is the number?

Solution

Steps 1-2 We first write what we want to find (a number) as a word phrase. Then, we use a variable to represent this number.

The number: x

Step 3 A sketch is not applicable in this problem.

Step 4 We write an equation relating the known and unknown quantities.

x + 9 - 4x

Step 5 We now solve the resulting equation.

x + 9 - x = 4x - x

9 = 3x

3 = x

Step 6 The number is 3.

CONSECUTIVE INTEGERS

Some algebraic word problems involve the concepts of consecutive integers. Consecutive integers are integers that differ by 1 or - 1. For example, 3 and 4 are consecutive integers and -2 and -1 are consecutive integers. If x represents an integer, then the next consecutive integer is represented by x + 1.

Consecutive even integers are even integers that differ by 2 or -2. For example, 6 and 8 are consecutive even integers and -4 and -2 are consecutive even integers. If x represents an even integer, then the next consecutive even integer is represented by x + 2.

Consecutive odd integers are odd integers that differ by 2 or -2. For example, 5 and 7 are consecutive odd integers and -3 and -1 are consecutive odd integers. If x represents an odd integer, then the next consecutive odd integer is represented by x + 2.

Example 2 Follow the six steps listed on page 115 to solve the following word problem.

The sum of two consecutive odd integers is 12. What are the integers?

Solution

Steps 1-2 We first write what we want to find (the integers) as two word phrases.

Then, we use a variable to represent the integers. The smaller odd integer: x

The next consecutive odd integer: x + 2

Step 3 A sketch is not applicable in this problem.

Step 4 Next, we write an equation relating known and unknown quantities.

x + (x + 2) = 12

Step 5 We now solve the resulting equation.

x + x + 2 = 12

2x + 2 = 12

2x = 10

x = 5

Step 6 The integers are 5 and 5 + 2, or 7.

In the following example, a sketch is helpful.

Example 3 Follow the six steps listed on page 115 to solve the following word problem.

A board 186 centimeters long is cut into two pieces so that one piece is twice as long as the other. How long is each of the two pieces?

Solution Steps 1-2 We first write what we want to find (the lengths) as word phrases. Then, we use a variable to represent the lengths.

The smaller piece: x

The larger piece: 2x

Step 3 We now make a sketch and label dimensions.

Step 4 Writing an equation relating the known and the unknown quantities yields

x + 2x = 186

Step 5 We now solve the equation.

3x = 186

x = 62

Step 6 The smaller piece is 62 centimeters and the larger piece is 2(62) or 124 centimeters.