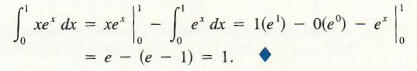Integration by Parts

Unlike differentiating, there is no systematic procedure for finding antiderivatives. The rule of substitution discussed in the previous section is effective if we can find a substitution u (x) for which a term u '(x) appears in the integral. Substitution may not work, but another powerful technique is available based on the product rule for derivatives. Integration by parts is given by the following formula.

To see this, note that



from the product rule for derivatives. Also,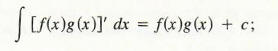



this statement about antiderivatives is true simply because the derivative of

Consequently,

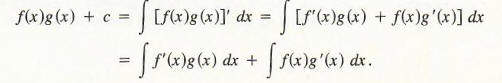
Thus,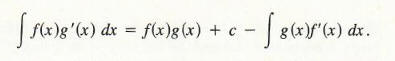


Since the antiderivative on the right side already involves a constant of integration,c is redundant and can be omitted. This gives us the formula for integrating by parts.

Remark: The g (x) in the integral on the right side of Formula (1) is any antiderivative of g '(x) in the integral on the left side; therefore, the constant in g (x) on the right side may be chosen to be any convenient value. It is usually chosen to be 0, although occasionally a different choice is useful.

Example 1 Find

To write this integral in the form

in order to apply Formula (1), we must determine how to choose f and g. The rule of thumb is to choose for g '(x) the "most difficult part" of the integrand which can be integrated. In this example, the rule suggests that we let g'(x) = e^x, and thus f(x) = x. With this choice,

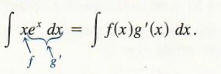
Clearly, f'(x) = I and g(x) = e^x. (Since g(x) is any antiderivative, we choose c = 0 in the general antiderivative e^x + c .) That is,

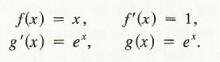
Hence,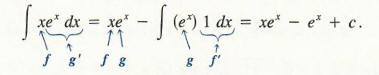


Example 2 Find

We have a choice to make: either let f(x) = ln(x) and g'(x) = 1 or let f(x) = 1 and g'(x) = ln(x). If we choose g'(x) = ln(x) and f(x) = l, we must then find g(x) by integrating ln(x), which is, unfortunately, exactly our problem in this example.
Hence, let f(x) = ln(x) and g'(x) = 1. Then f '(x) = 1/x and g(x) = x. We now have

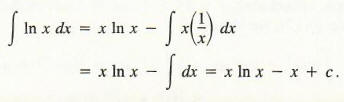
Example 3 Find

We could let g '(x) = ln(x) and use the result of Example 2, but then g (x) would be fairly complicated. Instead we let f(x) = ln(x) and g'(x) = x^1/2, in which case f '(x) = l/x and g(x) = 2/3x^3/2.Hence,

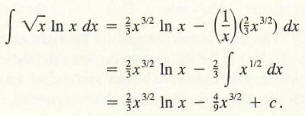
The next example illustrates how we can use integration by parts to evaluate a definite integral. The fundamental theorem of calculus is used together with the fact that the integration by parts formula changes one antiderivative into another. The integration by parts formula is

Hence, the corresponding formula for the definite integral is the following:

Example 4 Find

We begin by using the conventional techniques for integrating by parts. As in Example 1, let f(x) = x and g'(x) = e^x. Then f '(x) = 1 and g(x) = e^x, and hence, by Formula (3)