PRODUCTS AND FACTORS
THE DISTRIBUTIVE LAW
If we want to multiply a sum by another number, either we can multiply each term of the sum by the number before we add or we can first add the terms and then multiply. For example,
![]()
In either case the result is the same.
This property, which we first introduced in Section 1.8, is called the distributive law. In symbols,
a(b + c) = ab + ac or (b + c)a = ba + ca
By applying the distributive law to algebraic expressions containing parentheses, we can obtain equivalent expressions without parentheses.
Our first example involves the product of a monomial and binomial.
Example 1 Write 2x(x - 3) without parentheses.
Solution
We think of 2x(x - 3) as 2x[x + (-3)] and then apply the distributive law to obtain
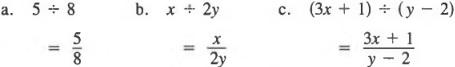
The above method works equally as well with the product of a monomial and trinomial.
Example 2 Write - y(y2 + 3y - 4) without parentheses.
Solution
Applying the distributive property yields
![]()
When simplifying expressions involving parentheses, we first remove the parentheses and then combine like terms.
Example 3 Simplify a(3 - a) - 2(a + a2).
We begin by removing parentheses to obtain
![]()
Now, combining like terms yields a - 3a2.
We can use the distributive property to rewrite expressions in which the coefficient of an expression in parentheses is +1 or - 1.
Example 4 Write each expression without parentheses.
a. +(3a - 2b)
b. -(2a - 3b)
Solution![]()
Notice that in Example 4b, the sign of each term is changed when the expression is written without parentheses. This is the same result that we would have obtained if we used the procedures that we introduced in Section 2.5 to simplify expressions.
FACTORING MONOMIALS FROM POLYNOMIALS
From the symmetric property of equality, we know that if
a(b + c) = ab + ac, then ab + ac = a(b + c)
Thus, if there is a monomial factor common to all terms in a polynomial, we can write the polynomial as the product of the common factor and another polynomial. For instance, since each term in x2 + 3x contains x as a factor, we can write the expression as the product x(x + 3). Rewriting a polynomial in this way is called factoring, and the number x is said to be factored "from" or "out of' the polynomial x2 + 3x.
To factor a monomial from a polynomial:
- Write a set of parentheses preceded by the monomial common to each term in the polynomial.
- Divide the monomial factor into each term in the polynomial and write the quotient in the parentheses.
Generally, we can find the common monomial factor by inspection.
Example 1
a. 4x + 4y = 4(x + y)
b. 3xy -6y - 3y(x - 2)
We can check that we factored correctly by multiplying the factors and verifying that the product is the original polynomial. Using Example 1, we get
![]()
If the common monomial is hard to find, we can write each term in prime factored form and note the common factors.
Example 2 Factor 4x3 - 6x2 + 2x.
Solution
We can write
![]()
We now see that 2x is a common monomial factor to all three terms. Then we factor 2x out of the polynomial, and write
2x( )
Now, we divide each term in the polynomial by 2x
![]()
and write the quotients inside the parentheses to get
2x(2x2 - 3x + 1)
We can check our answer in Example 2 by multiplying the factors to obtain
![]()
In this book, we will restrict the common factors to monomials consisting of numerical coefficients that are integers and to integral powers of the variables. The choice of sign for the monomial factor is a matter of convenience. Thus,
-3x2 - 6x
can be factored either as
-3x(x + 2) or as 3x(-x - 2)
The first form is usually more convenient.
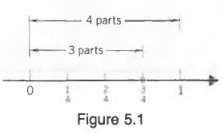
Example 3 Factor out the common monomial, including -1.
a. - 3x2 - 3 xy
b. -x3 - x2 + x
Solution
Sometimes it is convenient to write formulas in factored form.
Example 4
a. A = P + PRT
= P(1 + RT)
b. S = 4kR2 - 4kr2
= 4k(R2 - r2)
4.3 BINOMIAL PRODUCTS I
We can use the distributive law to multiply two binomials. Although there is little need to multiply binomials in arithmetic as shown in the example below, the distributive law also applies to expressions containing variables.
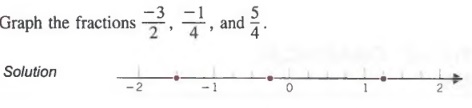
We will now apply the above procedure for an expression containing variables.
Example 1
Write (x - 2)(x + 3) without parentheses.
Solution
First, apply the distributive property to get
![]()
Now, combine like terms to obtain
x2 + x - 6
With practice, you will be able to mentally add the second and third products. Theabove process is sometimes called the FOIL method. F, O, I, and L stand for:
- 1. The product of the First terms.
- 2. The product of the Outer terms.
- 3. The product of the Inner terms.
- 4. The product of the Last terms.
The FOIL method can also be used to square binomials.
Example 2
Write (x + 3)2 without parentheses.
Solution
First, rewrite (x + 3)2 as (x + 3)(x + 3). Next, apply the FOIL method to get
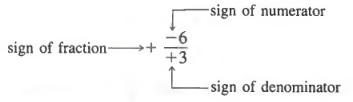
Combining like terms yields
x2 + 6x + 9
When we have a monomial factor and two binomial factors, it is easiest to first multiply the binomials.
Example 3
Write 3x(x - 2)(x + 3) without parentheses.
Solution
First, multiply the binomials to obtain
3x(x2 + 3x - 2x - 6) = 3x(x2 + x - 6)
Now, apply the distributive law to get
3x(x2 + x - 6) = 3x3 + 3x2 - 18x
Common Errors
Notice in Example 2
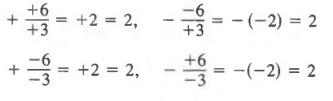
Similarly,
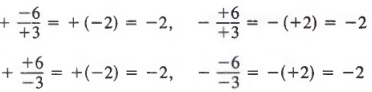
In general,

4.4 FACTORING TRINOMIALS I
In Section 4.3, we saw how to find the product of two binomials. Now we will reverse this process. That is, given the product of two binomials, we will find the binomial factors. The process involved is another example of factoring. As before,we will only consider factors in which the terms have integral numerical coefficients. Such factors do not always exist, but we will study the cases where they do.
Consider the following product.
![]()
Notice that the first term in the trinomial, x2, is product (1); the last term in the trinomial, 12, is product and the middle term in the trinomial, 7x, is the sum of products (2) and (3). In general,
![]()
We use this equation (from right to left) to factor any trinomial of the form x2 + Bx + C. We find two numbers whose product is C and whose sum is B.
Example 1 Factor x2 + 7x + 12.
Solution
We look for two integers whose product is 12 and whose sum is 7. Consider the following pairs of factors whose product is 12.
![]()
We see that the only pair of factors whose product is 12 and whose sum is 7 is 3 and 4. Thus,
x2 + 7x + 12 = (x + 3)(x + 4)
Note that when all terms of a trinomial are positive, we need only consider pairs of positive factors because we are looking for a pair of factors whose product and sum are positive. That is, the factored term of
x2 + 7x + 12 would be of the form
( + )( + )
When the first and third terms of a trinomial are positive but the middle term is negative, we need only consider pairs of negative factors because we are looking for a pair of factors whose product is positive but whose sum is negative. That is,the factored form of
x2 - 5x + 6
would be of the form
(-)(-)
Example 2 Factor x2 - 5x + 6.
Solution
Because the third term is positive and the middle term is negative, we find two negative integers whose product is 6 and whose sum is -5. We list the possibilities.
![]()
We see that the only pair of factors whose product is 6 and whose sum is -5 is -3 and -2. Thus,
x2 - 5x + 6 = (x - 3)(x - 2)
When the first term of a trinomial is positive and the third term is negative,the signs in the factored form are opposite. That is, the factored form of
x2 - x - 12
would be of the form
( + )( - ) or ( - )( + )
Example 3
Factor x2 - x - 12.
Solution We must find two integers whose product is -12 and whose sum is -1. We list the possibilities.
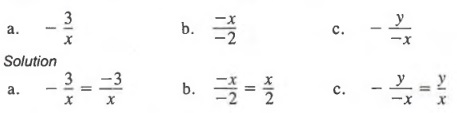
We see that the only pair of factors whose product is -12 and whose sum is -1 is -4 and 3. Thus,
x2 - x - 12 = (x - 4)(x + 3)
It is easier to factor a trinomial completely if any monimial factor common to each term of the trinomial is factored first. For example, we can factor
12x2 + 36x + 24
as
![]()
A monomial can then be factored from these binomial factors. However, first factoring the common factor 12 from the original expression yields
12(x2 + 3x + 2)
Factoring again, we have
12(* + 2)(x + 1)
which is said to be in completely factored form. In such cases, it is not necessary to factor the numerical factor itself, that is, we do not write 12 as 2 * 2 * 3.
Example 4
Factor 3x2 + 12x + 12 completely.
Solution
First we factor out the 3 from the trinomial to get
3(x2 + 4x + 4)
Now, we factor the trinomial and obtain
3(x + 2)(x + 2)
The techniques we have developed are also valid for a trinomial such as x2 + 5xy + 6y2.
Example 5Factor x2 + 5xy + 6y2.
Solution
We find two positive factors whose product is 6y2 and whose sum is 5y (the coefficient of x). The two factors are 3y and 2y. Thus,
x2 + 5xy + 6y2 = (x + 3y)(x + 2y)
When factoring, it is best to write the trinomial in descending powers of x. If the coefficient of the x2-term is negative, factor out a negative before proceeding.
Example 6
Factor 8 + 2x - x2.
Solution
We first rewrite the trinomial in descending powers of x to get
-x2 + 2x + 8
Now, we can factor out the -1 to obtain
-(x2 - 2x - 8)
Finally, we factor the trinomial to yield
-(x- 4)(x + 2)
Sometimes, trinomials are not factorable.
Example 7
Factor x2 + 5x + 12.
Solution
We look for two integers whose product is 12 and whose sum is 5. From the table in Example 1 on page 149, we see that there is no pair of factors whose product is 12 and whose sum is 5. In this case, the trinomial is not factorable.
Skill at factoring is usually the result of extensive practice. If possible, do the factoring process mentally, writing your answer directly. You can check the results of a factorization by multiplying the binomial factors and verifying that the product is equal to the given trinomial.
4.5 BINOMIAL PRODUCTS II
In this section, we use the procedure developed in Section 4.3 to multiply binomial factors whose first-degree terms have numerical coefficients other than 1 or - 1.
Example 1
Write as a polynomial.
a. (2x - 3)(x + 1)
b. (3x - 2y)(3x + y)
Solution
We first apply the FOIL method and then combine like terms.
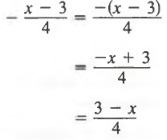
As before, if we have a squared binomial, we first rewrite it as a product, then apply the FOIL method.
Example 2
a. (3x + 2)2
= (3x + 2)(3x + 2)
= 9x2 + 6x + 6x + 4
= 9x2 + 12x + 4
b. (2x - y)2
= (2x - y)(2x - y)
= 4x2 - 2xy - 2xy + y2
- 4x2 - 4xy + y2
As you may have seen in Section 4.3, the product of two bionimals may have no first-degree term in the answer.
Example 3
a. (2x - 3)(2x + 3)
= 4x2 + 6x - 6x - 9
= 4x2 -9
b. (3x - y)(3x + y)
- 9x2 + 3xy - 3xy - y2 = 9x2 - y2
When a monomial factor and two binomial factors are being multiplied, it is easiest to multiply the binomials first.
Example 4
Write 3x(2x - l)(x + 2) as a polynomial.
Solution
We first multiply the binomials to get 3x(2x2 + 4x - x - 2) = 3x(2x2 + 3x - 2)
Now multiplying by the monomial yields 3x(2x2) + 3x(3x) + 3x(-2) = 6x3 + 9x2 - 6x
4.6 FACTORING TRINOMIALS II
In Section 4.4 we factored trinomials of the form x2 + Bx + C where the second- degree term had a coefficient of 1. Now we want to extend our factoring techniques to trinomials of the form Ax2 + Bx + C, where the second-degree term has a coefficient other than 1 or -1.
First, we consider a test to determine if a trinomial is factorable. A trinomial of the form Ax2 + Bx + C is factorable if we can find two integers whose product is A * C and whose sum is B.
Example 1
Determine if 4x2 + 8x + 3 is factorable.
Solution
We check to see if there are two integers whose product is (4)(3) = 12 and whose sum is 8 (the coefficient of x). Consider the following possibilities.
![]()
Since the factors 6 and 2 have a sum of 8, the value of B in the trinomial Ax2 + Bx + C, the trinomial is factorable.
Example 2
The trinomial 4x2 - 5x + 3 is not factorable, since the above table shows that there is no pair of factors whose product is 12 and whose sum is -5. The test to see if the trinomial is factorable can usually be done mentally.
Once we have determined that a trinomial of the form Ax2 + Bx + C is fac- torable, we proceed to find a pair of factors whose product is A, a pair of factors whose product is C, and an arrangement that yields the proper middle term. We illustrate by examples.
Example 3
Factor 4x2 + 8x + 3.
Solution
Above, we determined that this polynomial is factorable. We now proceed.
![]()
1. We consider all pairs of factors whose product is 4. Since 4 is positive, only positive integers need to be considered. The possibilities are 4, 1 and 2, 2.
2. We consider all pairs of factors whose product is 3. Since the middle term is positive, consider positive pairs of factors only. The possibilities are 3, 1. We write all possible arrangements of the factors as shown.
![]()
3. We select the arrangement in which the sum of products (2) and (3) yields a middle term of 8x.
Now, we consider the factorization of a trinomial in which the constant term is negative.
Example 4
Factor 6x2 + x - 2.
Solution
First, we test to see if 6x2 + x - 2 is factorable. We look for two integers that have a product of 6(-2) = -12 and a sum of 1 (the coefficient of x). The integers 4 and -3 have a product of -12 and a sum of 1, so the trinomial is factorable. We now proceed.
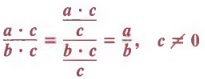
- We consider all pairs of factors whose product is 6. Since 6 is positive, only positive integers need to be considered. Then possibilities are 6, 1 and 2, 3.
- We consider all pairs of factors whose product is -2. The possibilities are 2, -1 and -2, 1. We write all possible arrange ments of the factors as shown.
- We select the arrangement in which the sum of products (2) and (3) yields a middle term of x.
With practice, you will be able to mentally check the combinations and will not need to write out all the possibilities. Paying attention to the signs in the trinomial is particularly helpful for mentally eliminating possible combinations.
It is easiest to factor a trinomial written in descending powers of the variable.
Example 5
Factor.
a. 3 + 4x2 + 8x
b. x - 2 + 6x2
Solution
Rewrite each trinomial in descending powers of x and then follow the solutions of Examples 3 and 4.
a. 4x2 + 8x + 3
b. 6x2 + x - 2
As we said in Section 4.4, if a polynomial contains a common monomial factor in each of its terms, we should factor this monomial from the polynomial before looking for other factors.
Example 6
Factor 242 - 44x - 40.
Solution
We first factor 4 from each term to get
4(6x2 - 11x - 10)
We then factor the trinomial, to obtain
4(3x + 2)(2x - 5)
ALTERNATIVE METHOD OF FACTORING TRINOMIALS
If the above "trial and error" method of factoring does not yield quick results, an alternative method, which we will now demonstrate using the earlier example 4x2 + 8x + 3, may be helpful.
We know that the trinomial is factorable because we found two numbers whose product is 12 and whose sum is 8. Those numbers are 2 and 6. We now proceed and use these numbers to rewrite 8x as 2x + 6x.
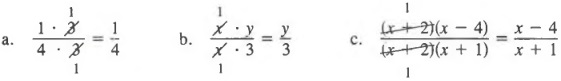
We now factor the first two terms, 4*2 + 2x and the last two terms, 6x + 3.
A common factor, 2x + 1, is in each term, so we can factor again.
This is the same result that we obtained before.
4.7 FACTORING THE DIFFERENCE OF TWO SQUARES
Some polynomials occur so frequently that it is helpful to recognize these special forms, which in tum enables us to directly write their factored form. Observe that
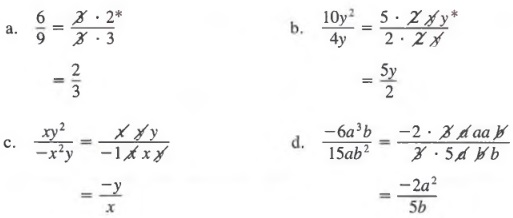
In this section we are interested in viewing this relationship from right to left, from the polynomial a2 - b2 to its factored form (a + b)(a - b).
The difference of two squares, a2 - b2, equals the product of the sum a + b and the difference a - b.
Example 1
a. x2 - 9 = x2 - 32
= (x + 3)(x - 3)
b. x2 - 16 = x2 - 42
= (x + 4)(x - 4)
Since
(3x)(3x) = 9x2
we can view a binomial such as 9x2 - 4 as (3x)2 - 22 and use the above method to factor.
Example 2
a. 9x2 - 4 = (3x)2 - 22
= (3x + 2)(3x - 2)
b. 4y2 - 25x2 = (2y)2 - (5x)2 = (2y + 5x)(2y - 5x)
As before, we always factor out a common monomial first whenever possible.
Example 3
a. x3 - x5 = x3(l - x2)
= x3(1 + x)(l - x)
b. a2x2y - 16y = y(a2x2 - 16)
= y[(ax)2 - 42]
= y(ax - 4 )(ax + 4)
4.8 EQUATIONS INVOLVING PARENTHESES
Often we must solve equations in which the variable occurs within parentheses. We can solve these equations in the usual manner after we have simplified them by applying the distributive law to remove the parentheses.
Example 1
Solve 4(5 - y) + 3(2y - 1) = 3.
Solution
We first apply the distributive law to get
20 - 4y + 6y - 3 = 3
Now combining like terms and solving for y yields
2y + 17 = 3
2y = -14
y=-l
The same method can be applied to equations involving binomial products.
Example 2
Solve (x + 5)(x + 3) - x = x2 + 1.
Solution
First, we apply the FOIL method to remove parentheses and obtain
x2 + 8x + 15 - x = x2 + 1
Now, combining like terms and solving for x yields
x2 + 7x + 15 = x2 + 1
7x = -14
x = -2
4.9 WORD PROBLEMS INVOLVING NUMBERS
Parentheses are useful in representing products in which the variable is contained in one or more terms in any factor.
Example 1
One integer is three more than another. If x represents the smaller integer, represent in terms of x
a. The larger integer.
b. Five times the smaller integer.
c. Five times the larger integer.
Solution
a. x + 3
b. 5x
c. 5(x + 3)
Let us say we know the sum of two numbers is 10. If we represent one number by x, then the second number must be 10 - x as suggested by the following table.
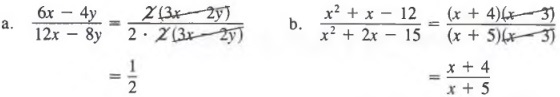
In general, if we know the sum of two numbers is 5 and x represents one number, the other number must be S - x.
Example 2
The sum of two integers is 13. If x represents the smaller integer, represent in terms of X
a. The larger integer.
b. Five times the smaller integer.
c. Five times the larger integer.
Solution
a. 13 - x
b. 5x
c. 5(13 - x)
The next example concerns the notion of consecutive integers that was consid- ered in Section 3.8.
Example 3
The difference of the squares of two consecutive odd integers is 24. If x represents the smaller integer, represent in terms of x
a. The larger integer
b. The square of the smaller integer
c. The square of the larger integer.
Solution
a. x + 2
b. x2
c. (x + 2)2
Sometimes, the mathematical models (equations) for word problems involve parentheses. We can use the approach outlined on page 115 to obtain the equation. Then, we proceed to solve the equation by first writing equivalently the equation without parentheses.
Example 4
One integer is five more than a second integer. Three times the smaller integer plus twice the larger equals 45. Find the integers.
Solution
Steps 1-2
First, we write what we want to find (the integers) as word phrases. Then, we represent the integers in terms of a variable.
The smaller integer: x
The larger integer: x + 5
Step 3
A sketch is not applicable.
Step 4
Now, we write an equation that represents the condition in the problem and get
3x + 2(x + 5) = 45
Step 5
Applying the distributive law to remove parentheses yields

Step 6
The integers are 7 and 7 + 5 or 12.
4.10 APPLICATIONS
In this section, we will examine several applications of word problems that lead to equations that involve parentheses. Once again, we will follow the six steps out- lined on page 115 when we solve the problems.
COIN PROBLEMS
The basic idea of problems involving coins (or bills) is that the value of a number of coins of the same denomination is equal to the product of the value of a single coin and the total number of coins.
![]()
A table like the one shown in the next example is helpful in solving coin problems.
Example 1
A collection of coins consisting of dimes and quarters has a value of $5.80. There are 16 more dimes than quarters. How many dimes and quarters are in the col- lection?
Solution
Steps 1-2 We first write what we want to find as word phrases. Then, we represent each phrase in terms of a variable.
The number of quarters: x
The number of dimes: x + 16
Step 3 Next, we make a table showing the number of coins and their value.
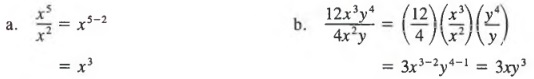
Step 4 Now we can write an equation.

Step 5 Solving the equation yields
![]()
Step 6 There are 12 quarters and 12 + 16 or 28 dimes in the collection.
INTEREST PROBLEMS
The basic idea of solving interest problems is that the amount of interest i earned in one year at simple interest equals the product of the rate of interest r and the amount of money p invested (i = r * p). For example, $1000 invested for one year at 9% yields i = (0.09)(1000) = $90.
A table like the one shown in the next example is helpful in solving interest problems.
Example 2
Two investments produce an annual interest of $320. $1000 more is invested at 11% than at 10%. How much is invested at each rate?
Solution
Steps 1-2 We first write what we want to find as word phrases. Then, we represent each phrase in terms of a variable.
Amount invested at 10%: x
Amount invested at 11%: x + 100
Step 3 Next, we make a table showing the amount of money invested, the rates of interest, and the amounts of interest.
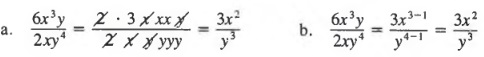
Step 4 Now, we can write an equation relating the interest from each in- vestment and the total interest received.
![]()
Step 5 To solve for x, first multiply each member by 100 to obtain
![]()
Step 6 $1000 is invested at 10%; $1000 + $1000, or $2000, is invested at 11%.
MIXTURE PROBLEMS
The basic idea of solving mixture problems is that the amount (or value) of the substances being mixed must equal the amount (or value) of the final mixture.
A table like the ones shown in the following examples is helpful in solving mixture problems.
Example 3
How much candy worth 80c a kilogram (kg) must a grocer blend with 60 kg of candy worth $1 a kilogram to make a mixture worth 900 a kilogram?
Solution
Steps 1-2 We first write what we want to find as a word phrase. Then, we represent the phrase in terms of a variable.
Kilograms of 80c candy: x
Step 3 Next, we make a table showing the types of candy, the amount of each, and the total values of each.
![]()
Step 4 We can now write an equation.
![]()
Step 5 Solving the equation yields
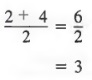
Step 6 The grocer should use 60 kg of the 800 candy.
Another type of mixture problem is one that involves the mixture of the two liquids.
Example 4
How many quarts of a 20% solution of acid should be added to 10 quarts of a 30% solution of acid to obtain a 25% solution?
Solution
Steps 1-2 We first write what we want to find as a word phrase. Then, we represent the phrase in terms of a variable.
Number of quarts of 20% solution to be added: x
Step 3 Next, we make a table or drawing showing the percent of each solu- tion, the amount of each solution, and the amount of pure acid in each solution.
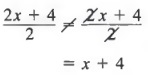
![]()
Step 4 We can now write an equation relating the amounts of pure acid before and after combining the solutions.
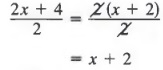
Step 5 To solve for x, first multiply each member by 100 to obtain
20x + 30(10) = 25(x + 10)
20x + 300 = 25x + 250
50 = 5x
10 = x
Step 6 Add 10 quarts of 20% solution to produce the desired solution.
CHAPTER SUMMARY
-
Algebraic expressions containing parentheses can be written without parentheses by applying the distributive law in the form
a(b + c) = ab + acA polynomial that contains a monomial factor common to all terms in the polynomial can be written as the product of the common factor and another polynomial by applying the distributive law in the form
ab + ac = a(b + c) -
The distributive law can be used to multiply binomials; the FOIL method suggests the four products involved.
![]()
-
Given a trinomial of the form x2 + Bx + C, if there are two numbers, a and b, whose product is C and whose sum is B, then
x2 + Bx + C = (x + a)(x + b)
otherwise, the trinomial is not factorable. -
A trinomial of the form Ax2 + Bx + C is factorable if there are two numbers whose product is A * C and whose sum is B.
-
The difference of squares
a2 - b2 = (a + b)(a - b) -
Equations involving parentheses can be solved in the usual way after the equation has been rewritten equivalently without parentheses.