QuickMath Download on App Store Download on Google Play
Welcome to Quickmath Solvers! Download on App Store Download on Google Play
Factor an expression.

Example: x^2+5x+6

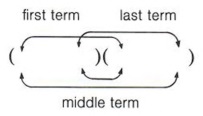
Factoring

The process of factoring is essential to the simplification of many algebraic expressions and is a useful tool in solving higher degree equations. In fact, the process of factoring is so important that very little of algebra beyond this point can be accomplished without understanding it.

In earlier chapters the distinction between terms and factors has been stressed. You should remember that terms are added or subtracted and factors are multiplied. Three important definitions follow.

Terms occur in an indicated sum or difference. Factors occur in an indicated product.

An expression is in factored form only if the entire expression is an indicated product.

Note in these examples that we must always regard the entire expression. Factors can be made up of terms and terms can contain factors, but factored form must conform to the definition above.

Factoring is a process of changing an expression from a sum or difference of terms to a product of factors.

Note that in this definition it is implied that the value of the expression is not changed - only its form.

REMOVING COMMON FACTORS

OBJECTIVES

Upon completing this section you should be able to:

  1. Determine which factors are common to all terms in an expression.
  2. Factor common factors.

In the previous chapter we multiplied an expression such as 5(2x + 1) to obtain 10x + 5. In general, factoring will "undo" multiplication. Each term of 10x + 5 has 5 as a factor, and 10x + 5 = 5(2x + 1).

To factor an expression by removing common factors proceed as in example 1.

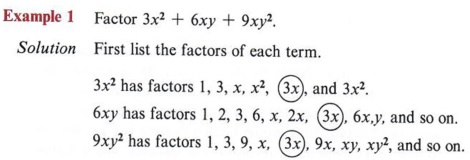
3x is the greatest common factor of all three terms.

Next look for factors that are common to all terms, and search out the greatest of these. This is the greatest common factor. In this case, the greatest common factor is 3x.

Proceed by placing 3x before a set of parentheses.

The terms within the parentheses are found by dividing each term of the original expression by 3x.

Note that this is the distributive property. It is the reverse of the process that we have been using until now.

The original expression is now changed to factored form. To check the factoring keep in mind that factoring changes the form but not the value of an expression. If the answer is correct, it must be true that . Multiply to see that this is true. A second check is also necessary for factoring - we must be sure that the expression has been completely factored. In other words, "Did we remove all common factors? Can we factor further?"

If we had only removed the factor "3" from 3x2 + 6xy + 9xy2, the answer would be

3(x2 + 2xy + 3xy2).

Multiplying to check, we find the answer is actually equal to the original expression. However, the factor x is still present in all terms. Hence, the expression is not completely factored.

This expression is factored but not completely factored.

For factoring to be correct the solution must meet two criteria:

  1. It must be possible to multiply the factored expression and get the original expression.
  2. FThe expression must be completely factored.

Example 2 Factor 12x3 + 6x2 + 18x.

Solution

At this point it should not be necessary to list the factors of each term. You should be able to mentally determine the greatest common factor. A good procedure to follow is to think of the elements individually. In other words, don’t attempt to obtain all common factors at once but get first the number, then each letter involved. For instance, 6 is a factor of 12, 6, and 18, and x is a factor of each term. Hence 12x3 + 6x2 + 18x = 6x(2x2 + x + 3). Multiplying, we get the original and can see that the terms within the parentheses have no other common factor, so we know the solution is correct.

Say to yourself, "What is the largest common factor of 12, 6, and 18?"

Then, "What is the largest common factor of x3, x2, and x?"

Remember, this is a check to make sure we have factored correctly.

Again, multiply out as a check.

Again, find the greatest common factor of the numbers and each letter separately.

If an expression cannot be factored it is said to be prime.

Remember that 1 is always a factor of any expression.

FACTORING BY GROUPING

OBJECTIVES

Upon completing this section you should be able to:

  1. Factor expressions when the common factor involves more than one term.
  2. Factor by grouping.

An extension of the ideas presented in the previous section applies to a method of factoring called grouping.

First we must note that a common factor does not need to be a single term. For instance, in the expression 2y(x + 3) + 5(x + 3) we have two terms. They are 2y(x + 3) and 5(x + 3). In each of these terms we have a factor (x + 3) that is made up of terms. This factor (x + 3) is a common factor.

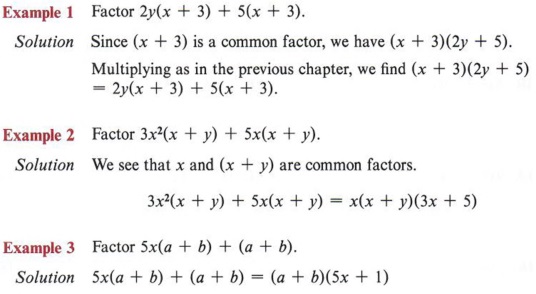
Sometimes when there are four or more terms, we must insert an intermediate step or two in order to factor.

Solution

First note that not all four terms in the expression have a common factor, but that some of them do. For instance, we can factor 3 from the first two terms, giving 3(ax + 2y). If we factor a from the remaining two terms, we get a(ax + 2y). The expression is now 3(ax + 2y) + a(ax + 2y), and we have a common factor of (ax + 2y) and can factor as (ax + 2y)(3 + a). Multiplying (ax + 2y)(3 + a), we get the original expression 3ax + 6y + a2x + 2ay and see that the factoring is correct.

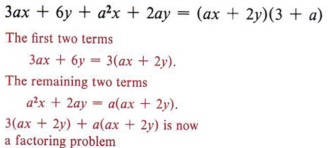
This is an example of factoring by grouping since we "grouped" the terms two at a time.

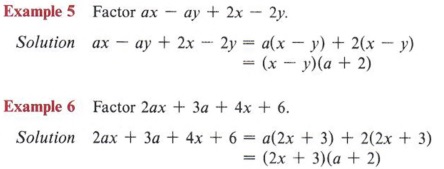
Multiply (x - y)(a + 2) and see if you get the original expression.
Again, multiply as a check.

Sometimes the terms must first be rearranged before factoring by grouping can be accomplished.

Example 7 Factor 3ax + 2y + 3ay + 2x.

Solution

The first two terms have no common factor, but the first and third terms do, so we will rearrange the terms to place the third term after the first. Always look ahead to see the order in which the terms could be arranged.

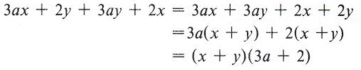
In all cases it is important to be sure that the factors within parentheses are exactly alike. This may require factoring a negative number or letter.

Remember, the commutative property allows us to rearrange these terms.
Multiply as a check.

Example 8 Factor ax - ay - 2x + 2y.

Solution

Note that when we factor a from the first two terms, we get a(x - y). Looking at the last two terms, we see that factoring +2 would give 2(-x + y) but factoring "-2" gives - 2(x - y). We want the terms within parentheses to be (x - y), so we proceed in this manner.

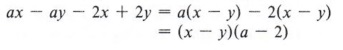
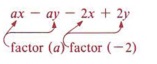
FACTORING TRINOMIALS

OBJECTIVES

Upon completing this section you should be able to:

  1. Mentally multiply two binomials.
  2. Factor a trinomial having a first term coefficient of 1.
  3. Find the factors of any factorable trinomial.

A large number of future problems will involve factoring trinomials as products of two binomials. In the previous chapter you learned how to multiply polynomials. We now wish to look at the special case of multiplying two binomials and develop a pattern for this type of multiplication.

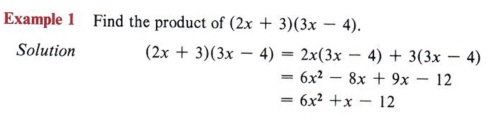
Since this type of multiplication is so common, it is helpful to be able to find the answer without going through so many steps. Let us look at a pattern for this.

From the example (2x + 3)(3x - 4) = 6x2 + x - 12, note that the first term of the answer (6x2) came from the product of the two first terms of the factors, that is (2x)(3x).

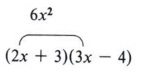
Also note that the third term (-12) came from the product of the second terms of the factors, that is ( + 3)(-4).

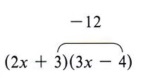
We now have the following part of the pattern:

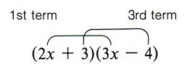
Now looking at the example again, we see that the middle term (+x) came from a sum of two products (2x)( -4) and (3)(3x).

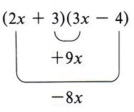
For any two binomials we now have these four products:

  1. First term by first term
  2. Outside terms
  3. Inside terms
  4. Last term by last term

These products are shown by this pattern.

When the products of the outside terms and inside terms give like terms, they can be combined and the solution is a trinomial.

This method of multiplying two binomials is sometimes called the FOIL method.
FOIL stands for First, Outer, Inner, Last.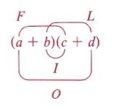

It is a shortcut method for multiplying two binomials and its usefulness will be seen when we factor trinomials.

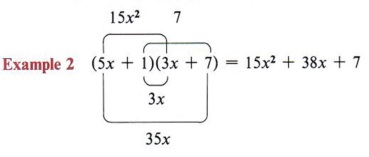
You should memorize this pattern.

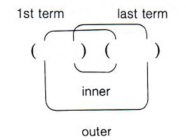
Again, maybe memorizing the word FOIL will help.

Not only should this pattern be memorized, but the student should also learn to go from problem to answer without any written steps. This mental process of multiplying is necessary if proficiency in factoring is to be attained.

As you work the following exercises, attempt to arrive at a correct answer without writing anything except the answer. The more you practice this process, the better you will be at factoring.

Now that we have established the pattern of multiplying two binomials, we are ready to factor trinomials. We will first look at factoring only those trinomials with a first term coefficient of 1.

Solution

Since this is a trinomial and has no common factor we will use the multiplication pattern to factor.

We will actually be working in reverse the process developed in the last exercise set.

First write parentheses under the problem.

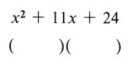
We now wish to fill in the terms so that the pattern will give the original trinomial when we multiply. The first term is easy since we know that (x)(x) = x2.

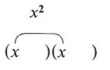
Remember, the product of the first two terms of the binomials gives the first term of the trinomial.

We must now find numbers that multiply to give 24 and at the same time add to give the middle term. Notice that in each of the following we will have the correct first and last term.

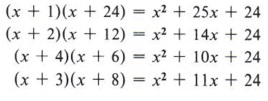
Only the last product has a middle term of 11x, and the correct solution is

This method of factoring is called trial and error - for obvious reasons.

Some number facts from arithmetic might be helpful here.
  1. The product of two odd numbers is odd.
  2. The product of two even numbers is even.
  3. The product of an odd and an even number is even.
  4. The sum of two odd numbers is even.
  5. The sum of two even numbers is even.
  6. The sum of an odd and even number is odd.
Therefore, when we factor an expression such as x2 + 11x + 24, we know that the product of the last two terms in the binomials must be 24, which is even, and their sum must be 11, which is odd.
Thus, only an odd and an even number will work. We need not even try combinations like 6 and 4 or 2 and 12, and so on.

Solution

Here the problem is only slightly different. We must find numbers that multiply to give 24 and at the same time add to give - 11. You should always keep the pattern in mind. The last term is obtained strictly by multiplying, but the middle term comes finally from a sum. Knowing that the product of two negative numbers is positive, but the sum of two negative numbers is negative, we obtain

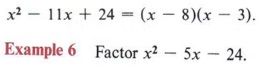
Solution

We are here faced with a negative number for the third term, and this makes the task slightly more difficult. Since -24 can only be the product of a positive number and a negative number, and since the middle term must come from the sum of these numbers, we must think in terms of a difference. We must find numbers whose product is 24 and that differ by 5. Furthermore, the larger number must be negative, because when we add a positive and negative number the answer will have the sign of the larger. Keeping all of this in mind, we obtain

The order of factors is insignificant.

by the commutative law of multiplication.

The following points will help as you factor trinomials:

  1. When the sign of the third term is positive, both signs in the factors must be alike-and they must be like the sign of the middle term.
  2. When the sign of the last term is negative, the signs in the factors must be unlike-and the sign of the larger must be like the sign of the middle term.

In the previous exercise the coefficient of each of the first terms was 1. When the coefficient of the first term is not 1, the problem of factoring is much more complicated because the number of possibilities is greatly increased.

Having done the previous exercise set, you are now ready to try some more challenging trinomials.

Notice that there are twelve ways to obtain the first and last terms, but only one has 17x as a middle term.

You could, of course, try each of these mentally instead of writing them out.

There is only one way to obtain all three terms:

In this example one out of twelve possibilities is correct. Thus trial and error can be very time-consuming.

Even though the method used is one of guessing, it should be "educated guessing" in which we apply all of our knowledge about numbers and exercise a great deal of mental arithmetic. In the preceding example we would immediately dismiss many of the combinations. Since we are searching for 17x as a middle term, we would not attempt those possibilities that multiply 6 by 6, or 3 by 12, or 6 by 12, and so on, as those products will be larger than 17. Also, since 17 is odd, we know it is the sum of an even number and an odd number. All of these things help reduce the number of possibilities to try.

First find numbers that give the correct first and last terms of the trinomial. Then add the outer and inner product to check for the proper middle term.

Solution

First we should analyze the problem.

  1. The last term is positive, so two like signs.
  2. The middle term is negative, so both signs will be negative.
  3. The factors of 6x2 are x, 2x, 3x, 6x. The factors of 15 are 1, 3, 5, 15.
  4. Eliminate as too large the product of 15 with 2x, 3x, or 6x. Try some reasonable combinations.

These would automatically give too large a middle term.

See how the number of possibilities is cut down.

Solution

Analyze:

  1. The last term is negative, so unlike signs.
  2. We must find products that differ by 5 with the larger number negative.
  3. We eliminate a product of 4x and 6 as probably too large.
  4. Try some combinations.

Remember, mentally try the various possible combinations that are reasonable. This is the process of "trial and error" factoring. You will become more skilled at this process through practice.

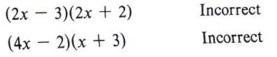
(4x - 3)(x + 2) : Here the middle term is + 5x, which is the right number but the wrong sign. Be careful not to accept this as the solution, but switch signs so the larger product agrees in sign with the middle term.

By the time you finish the following exercise set you should feel much more comfortable about factoring a trinomial.

SPECIAL CASES IN FACTORING

OBJECTIVES

Upon completing this section you should be able to:

  1. Identify and factor the differences of two perfect squares.
  2. Identify and factor a perfect square trinomial.

In this section we wish to examine some special cases of factoring that occur often in problems. If these special cases are recognized, the factoring is then greatly simplified.

The first special case we will discuss is the difference of two perfect squares.

Recall that in multiplying two binomials by the pattern, the middle term comes from the sum of two products.

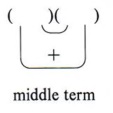
From our experience with numbers we know that the sum of two numbers is zero only if the two numbers are negatives of each other.

When the sum of two numbers is zero, one of the numbers is said to be the additive inverse of the other.
For example: ( + 3) + (-3) = 0, so + 3 is the additive inverse of - 3, also -3 is the additive inverse of +3.

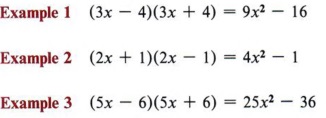
In each example the middle term is zero. Note that if two binomials multiply to give a binomial (middle term missing), they must be in the form of (a - b) (a + b).

The rule may be written as = (a - b)(a + b). This is the form you will find most helpful in factoring.

Reading this rule from right to left tells us that if we have a problem to factor and if it is in the form of , the factors will be (a - b)(a + b).

Solution

Here both terms are perfect squares and they are separated by a negative sign.

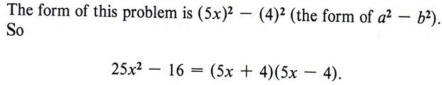
Where a = 5x and b = 4.

Special cases do make factoring easier, but be certain to recognize that a special case is just that-very special. In this case both terms must be perfect squares and the sign must be negative, hence "the difference of two perfect squares."

The sum of two squares is not factorable.

You must also be careful to recognize perfect squares. Remember that perfect square numbers are numbers that have square roots that are integers. Also, perfect square exponents are even.

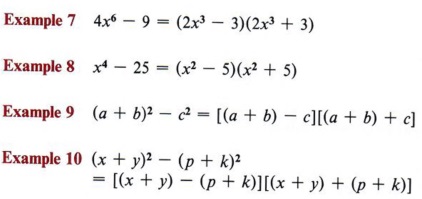
Students often overlook the fact that (1) is a perfect square. Thus, an expression such as x2 - 1 is the difference of two perfect squares and can be factored by this method.

Another special case in factoring is the perfect square trinomial. Observe that squaring a binomial gives rise to this case.

We recognize this case by noting the special features. Three things are evident.

  1. The first term is a perfect square.
  2. The third term is a perfect square.
  3. The middle term is twice the product of the square root of the first and third terms.

For factoring purposes it is more helpful to write the statement as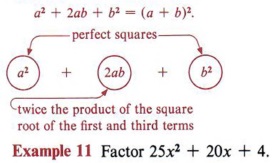

Solution

  1. 25x2 is a perfect square-principal square root = 5x.
  2. 4 is a perfect square-principal square root = 2.
  3. 20x is twice the product of the square roots of 25x2 and
  4. 20x = 2(5x)(2).

To factor a perfect square trinomial form a binomial with the square root of the first term, the square root of the last term, and the sign of the middle term, and indicate the square of this binomial.

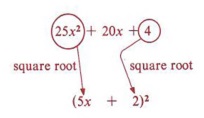
Thus, 25x2 + 20x + 4 = (5x + 2)2

Always square the binomial as a check to make sure the middle term is correct.

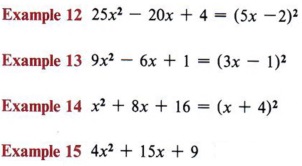
Not the special case of a perfect square trinomial.

15 ≠ 2(2x)(3)

OPTIONAL SHORTCUTS TO TRIAL AND ERROR FACTORING

OBJECTIVES

Upon completing this section you should be able to:

  1. Find the key number of a trinomial.
  2. Use the key number to factor a trinomial.

In this section we wish to discuss some shortcuts to trial and error factoring. These are optional for two reasons. First, some might prefer to skip these techniques and simply use the trial and error method; second, these shortcuts are not always practical for large numbers. However, they will increase speed and accuracy for those who master them.

The first step in these shortcuts is finding the key number. After you have found the key number it can be used in more than one way.

In a trinomial to be factored the key number is the product of the coefficients of the first and third terms.


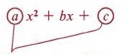The product of these two numbers is the "key number."

The first use of the key number is shown in example 3.

Solution
Step 1 Find the key number. In this example (4)(-10)= -40.
Step 2 Find factors of the key number (-40) that will add to give the coefficient of the middle term ( + 3). In this case ( + 8)( -5) = -40 and ( + 8) + (-5) = +3.
Step 3 The factors ( + 8) and ( - 5) will be the cross products in the multiplication pattern.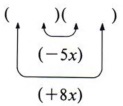


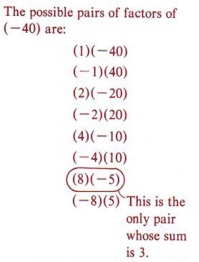The product of these two numbers is the "key number."

Step 4 Using only the outside cross product, find factors of the first and third terms that will multiply to give the product. In this example we must find factors of 4x2 and -10 that will multiply to give +8x. These are 4x from 4x2 and ( + 2) from (-10).
Place these factors in the first and last positions in the pattern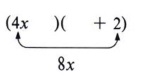

There is only one way it can be done correctly.

Step 5 Forget the key number at this point and look back at the original problem. Since the first and last positions are correctly filled, it is now only necessary to fill the other two positions.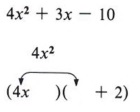

Again, this can be done in only one way.

We know the product of the two first terms must give 4x2 and 4x is already in place. There is no choice other than x.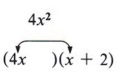

Note that in step 4 we could have started with the inside product instead of the outside product. We would have obtained the same factors. The most important thing is to have a systematic process for factoring.

We know that the product of the two second terms must be ( -10) and ( + 2) is already in place. We have no choice other than ( - 5).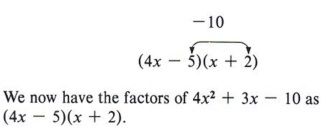

Remember, if a trinomial is factorable, there is only one possible set of factors.

If no factors of the key number can be found whose sum is the coefficient of the middle terms, then the trinomial is prime and does not factor.

A second use for the key number as a shortcut involves factoring by grouping. It works as in example 5.

Solution
Step 1 Find the key number (4)(-10) = -40.
Step 2 Find factors of ( - 40) that will add to give the coefficient of the middle term (+3).

Steps 1 and 2 in this method are the same as in the previous method.

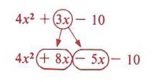
Step 3 Rewrite the original problem by breaking the middle term into the two parts found in step 2. 8x - 5x = 3x, so we may write

Step 4 Factor this problem from step 3 by the grouping method studied in section 8-2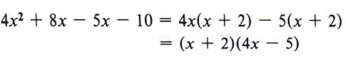


This now becomes a regular factoring by grouping problem.

Hence,
Again, there is only one possible pair of factors that can be obtained from a given trinomial.

Remember, if step 2 is impossible, the trinomial is prime and cannot be factored.

COMPLETE FACTORIZATION

OBJECTIVES

Upon completing this section you should be able to factor a trinomial using the following two steps:

  1. First look for common factors.
  2. Factor the remaining trinomial by applying the methods of this chapter.

We have now studied all of the usual methods of factoring found in elementary algebra. However, you must be aware that a single problem can require more than one of these methods. Remember that there are two checks for correct factoring.

  1. Will the factors multiply to give the original problem?
  2. Are all factors prime?

Once a common factor has been found, you must check to see if the resulting trinomial is factorable.

If a trinomial has any common factors, it is usually easier if they are factored first.

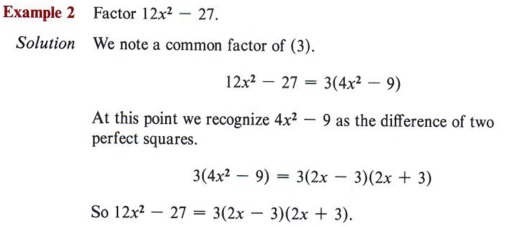
A good procedure to follow in factoring is to always remove the greatest common factor first and then factor what remains, if possible.

SUMMARY

Key Words

  • An expression is in factored form only if the entire expression is an indicated product.
  • Factoring is a process that changes a sum or difference of terms to a product of factors.
  • A prime expression cannot be factored.
  • The greatest common factor is the greatest factor common to all terms.
  • An expression is completely factored when no further factoring is possible.
  • The possibility of factoring by grouping exists when an expression contains four or more terms.
  • The FOIL method can be used to multiply two binomials.
  • Special cases in factoring include the difference of two squares and perfect square trinomials.
  • The key number is the product of the coefficients of the first and third terms of a trinomial.

Procedures

  • To remove common factors find the greatest common factor and divide each term by it.
  • Trinomials can be factored by using the trial and error method. This uses the pattern for multiplication to find factors that will give the original trinomial.
  • To factor the difference of two squares use the rule
  • To factor a perfect square trinomial form a binomial with the square root of the first term, the square root of the last term, and the sign of the middle term and indicate the square of this binomial.
  • Use the key number as an aid in determining factors whose sum is the coefficient of the middle term of a trinomial.