Example: 2x-1=y,2y+3=x
To see your tutorial, please scroll down
Ordered pairs, graphing linear equations, slope-intercept and point-slope forms
8.1 Ordered Pairs
Equations such as d=60t, {Iota}= 0.05P, and y = 2x + 3 represent relationships between pairs of variables. For example, in the first equation, if t = 3, than d = 60 * 3 = 180. With the understanding that t is first and d is second, we can write the pair (3, 180) to represent t = 3 and d = 180. The pair (8,180) is called an ordered pair. Obviously, (180, 3) is different from (3, 180) if t is the first number and d is the second number.
We say that (3, 180) satisfies the equation or is a solution of the equation d=60t. Similarly, (100, 5) satisfies {Iota}= 0.05P where P = 100 and {Iota}= 0.05(100)=5 . Also, (2, 7) satisfies y = 2x + 3 where x = 2 and y=2*2+3=7.
In an ordered pair, say (x, y), x is called the first component and y is called the second component. To find ordered pairs that satisfy an equation such as y = 2x + 3, we can choose any value for one variable, then find the corresponding value for the other variable by substituting into the equation. For example,
choose x=1, then y=2*1+3=5
choose x= -2, then y=2(-2)+3= -1
choose x=1/2, then y=2(1/2)+3=4
The ordered pairs (1,5), (-2, -1), and (1/2, 4) all satisfy the equation y = 2x + 3.
The variable assigned to the first component is also called the independent variable, and the variable assigned to the second component is called the dependent variable. Thus, we associate (x, y) with y = 2x + 3, and y “depends” on the values assigned to x.
We can also write the pairings in the form of tables. The choices for the values of the independent variable are arbitrary.
d=60t
| t | d |
| 5 | 60*5=300 |
| 10 | 60*10=600 |
| 12 | 60*12=720 |
| 15 | 60*15=900 |
{Iota}=0.5P
| P | {Iota} |
| 100 | 0.05*(100)=5 |
| 200 | 0.05(200)=10 |
| 500 | 0.05(500)=25 |
| 1000 | 0.05(1000)=50 |
y=2x+3
| x | y |
| -2 | 2(-2)+3=-1 |
| -1 | 2(-1)+3=1 |
| 0 | 2(0)+3=3 |
| 3 | 2(3)+3=9 |
Another notation commonly used in mathematics to represent the dependent variable is function notation. The symbol f (x) (read “f of x ”) is used to represent the value of the dependent variable related to x. For example,
if f(x)=2x-5
then f(1)=2*1-5=-3
f(3)=2*3-5=1
f(6)=2*6-5=7
and f(-1)=2(-1)-5=-7
(Note: f(x) does not mean to multiply f by x. f(x) is a notation unto itself.)
Due to the work of Rene Descartes (1596-1650), we can represent ordered pairs as points on a plane by graphing, using the Cartesian coordinate system. In this system, two number lines intersect at right angles and separate the plane into four quadrants. The origin, designated by the ordered pair (0, 0), is the point of intersection. The horizontal number line is called the horizontal axis or x-axis. The vertical number line is called the vertical axis or y-axis. Points that lie on either axis are not in any quadrant. They are simply on an axis (See Figure 8.1).
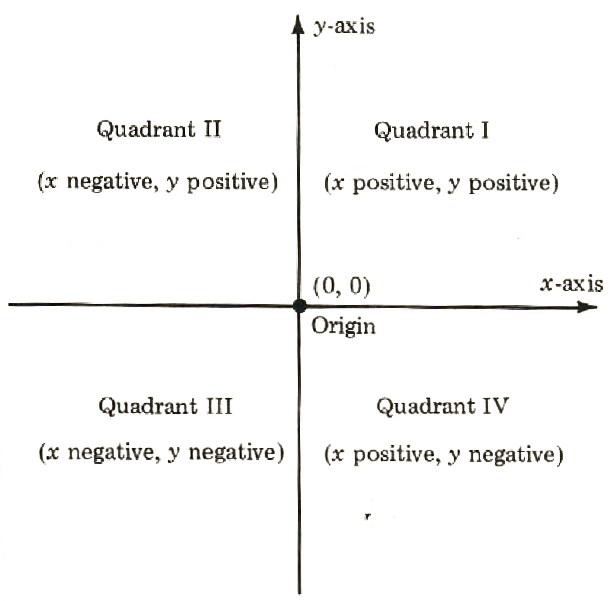
Figure 8.1
There is a one-to-one correspondence between points in a plane and ordered pairs of real numbers. In other words, for each point there is one corresponding ordered pair of real numbers, and for each ordered pair of real numbers there is one corresponding point. This important relationship is the cornerstone of the Cartesian coordinate system.
The graphs of the points A(2, 1), B(-2, 3), C(-3, -2), D(l, -2), and {Epsilon}=(3, 0) are shown in Figure 8.2. (Note: An ordered pair of real numbers and the corresponding point on the graph are frequently used to refer to each other. Thus, the ordered pair (2,1) and the point (2,1) are interchangeable ideas.)
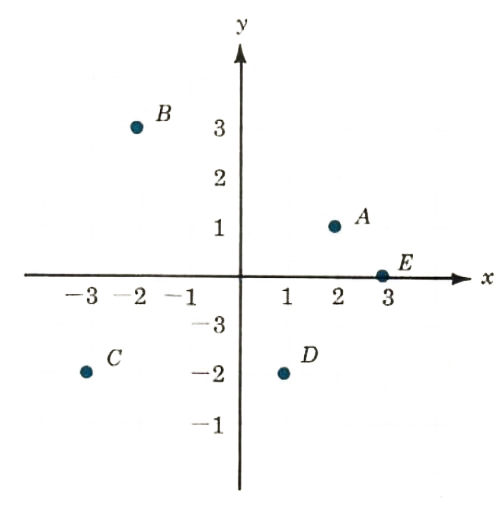
Figure 8.2
Examples
Graph the sets of ordered pairs in Examples 1 and 2
1. {(-2,1),(0, 2), (1,3), (2, -3)}
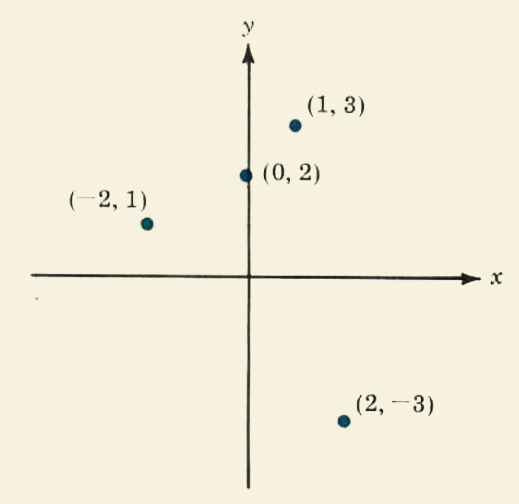
2. {(-1,3),(0,1),(1,-1),(2,-3),(3,-5)}
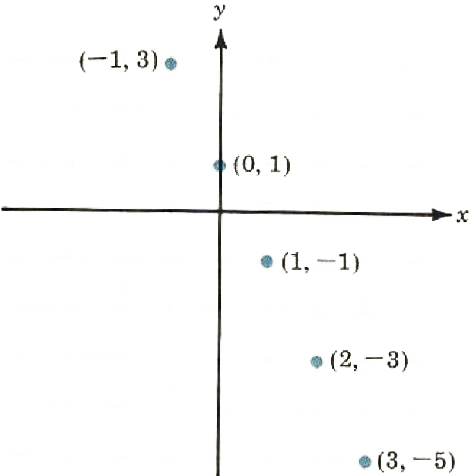
3. If f(x)=-2x+1, find f(-1),f(0),f(1),f(2), and f(3).
f(1)=-2(-1)+1=3
f(0)=-2(0)+1=1
f(1)=-2(1)+1=-1
f(2)=-2(2)+1=-3
f(3)=-2(3)+1=-5
8.2 Graphing Linear Equations
Suppose we want to graph the points that satisfy the equation y = 2x + 3. There is an infinite number of such points. We will graph five to try to find a pattern (See Figure 8.3).
The five points in Figure 8.3 appear to lie on a straight line. They in fact do lie on a straight line, and any ordered pair that satisfies the equation y = 2x + 3 will also lie on that same line.
What determines whether or not the points that satisfy an equation will lie on a straight line‘? The points that satisfy any equation of the form
Ax+By=C
will Lie on a straight line. The equation is called a linear equation and is considered the standard form for the equation of a line. We can write the equation y = 2x + 3 in the standard form -2x + y = 3.
| x | 2x+3=y |
| 0 | 2(0)+3=3 |
| -1 | 2(-1)+3=1 |
| 1/2 | 2(1/2)+3=4 |
| 1 | 2(1)+3=5 |
| -2 | 2(-2)+3=-1 |
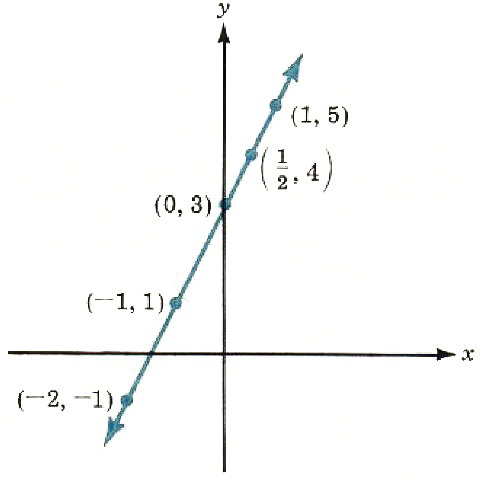
Figure 8.3
Since we now know that the graph will be a straight line, only two points are necessary to determine the entire graph. (Two points determine a line.) The choice of the two points depends on the choice of any two values of x or any two values of y.
Examples
1. Draw the graph of the linear equation x + 3y = 6.
x=0
0+3y=6
y=2
x=3
3+3y=6
3y=3
y=1
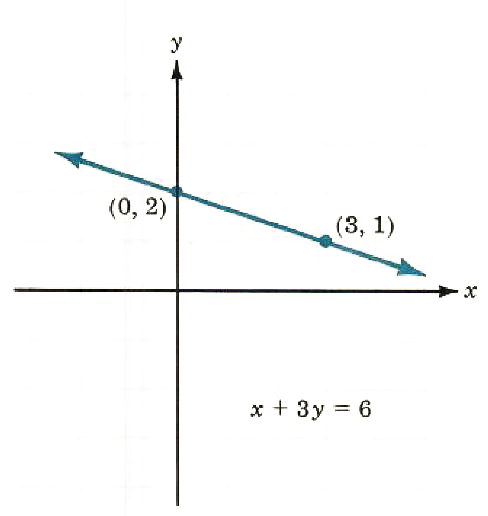Two points on the graph are (0, 2) and (3, 1). You may have chosen two others. Avoid choosing two points close together.
2. Draw the graph of the linear equation 2x-5y=10
x=5
2*5-5y=10
10-5y=10
-5y=10
y=0
x=0
2*0-5y=10
0-5y=10
y=-2
x=-5
2(-5)-5y=10
-10-5y=10
-5y=20
y=-4
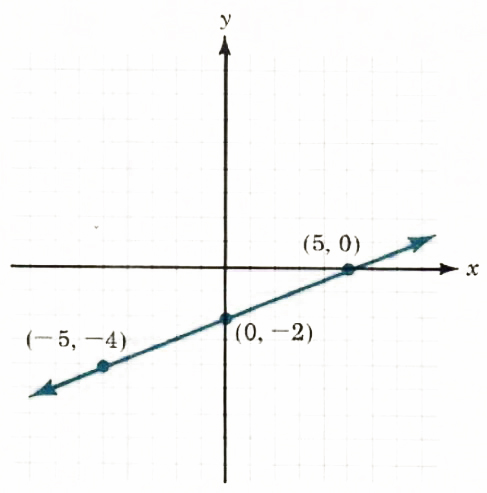Graphing three points is a good idea, simply to be sure the graph is in the right position.
While the choice of the values for x or y can be arbitrary, letting the value of x = 0 will locate the point on the graph where the line crosses the y-axis. This point is called the y-intercept. The x-intercept is the point found by letting y = 0. These two points are generally easy to locate and are frequently used as the two points for drawing the graph of a linear equation.
Examples
Graph the following linear equations by locating the x-intercepts and the
y-intercepts.
1. 3y+2x=6
x=0→y=2
y=0→x=3
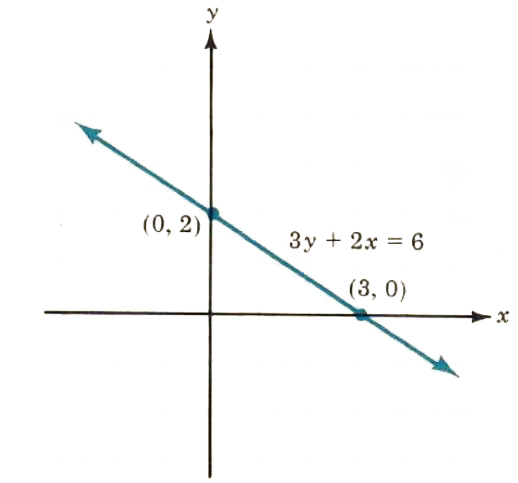
Let’s see how our math solver generates graph of this equation and similar linear equations. Click on "Solve Similar" button to see more examples.
2. 3y-2x=6
x=0→y=2
y=0→x=-3
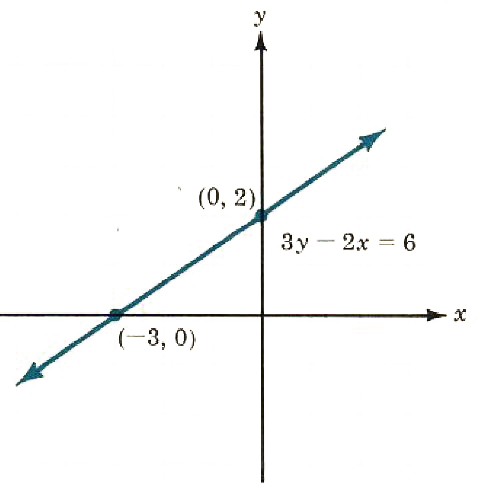
Since the x-coordinate of the y-intercept is always 0, We will agree to call the y-coordinate the y-intercept. In examples 1 and 2 just given, We will say the y-intercept is 2 rather than giving the coordinates (0, 2). Similarly, in example 1 the x-intercept is 3, and in example 2 the x-intercept is -3. If the line goes through the origin, both the x-intercept and the y-intercept will be 0. In this case, some other point must be used.
Example
Graph the following linear equation: y - 3x = 0
y-3x=0
x=0→y=0
x=2→y=6
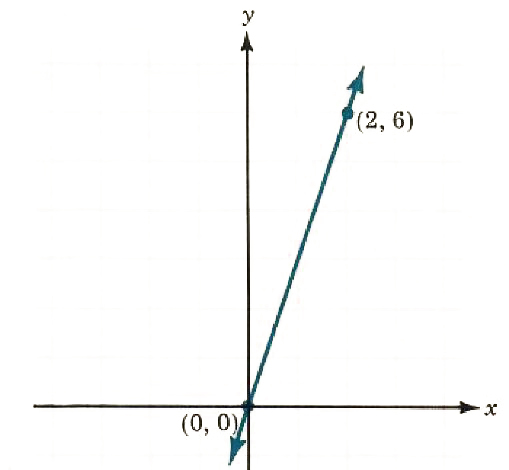
Let’s see how our math solver generates graph of this equation and similar linear equations. Click on "Solve Similar" button to see more examples.
8.3 Slope-Intercept and Point-Slope Forms
A carpenter is given a set of house plans that call for a 5:12 roof. What does this mean to the carpenter? This means that he must construct the roof so that for every 5 inches of rise (vertical distance), there are 12 inches of run (horizontal distance). That is, the ratio of rise to run is 5/12 (See Figure 8.4.)
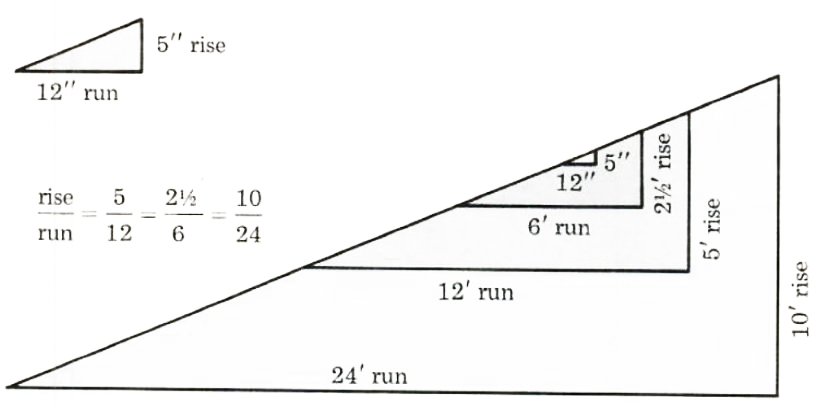
Figure 8.4
What if another roof is to be 7:12? Would the carpenter then construct the roof so that for every 7 inches of rise, there would be 12 inches of run? Of course. The ratio of rise to run would be 7/12 (See Figure 8.5.)
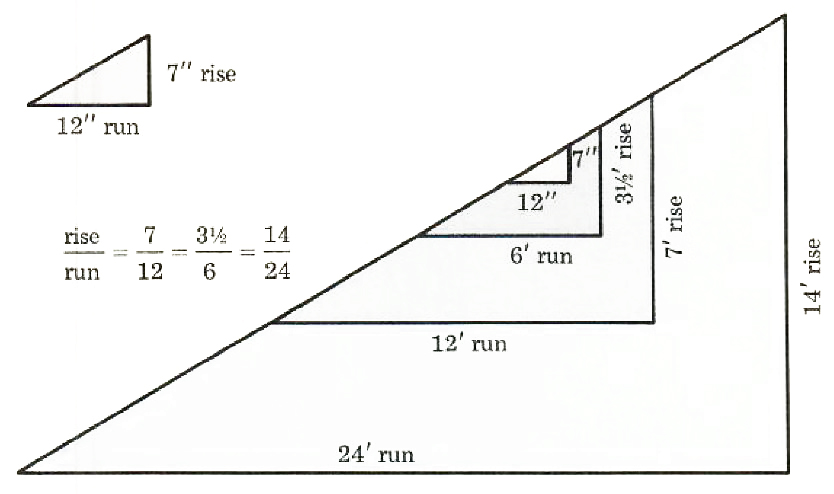
Figure 8.5
Other examples involving the ratio of rise to run are the slope of a road and the slope of the side of a ditch.
For a straight line, the ratio of rise to run is called the slope of the line.
slope=(rise)/(run)
The graph of the linear equation y=3x-1 is given in Figure 8.6 What do you think is the slope of the line?
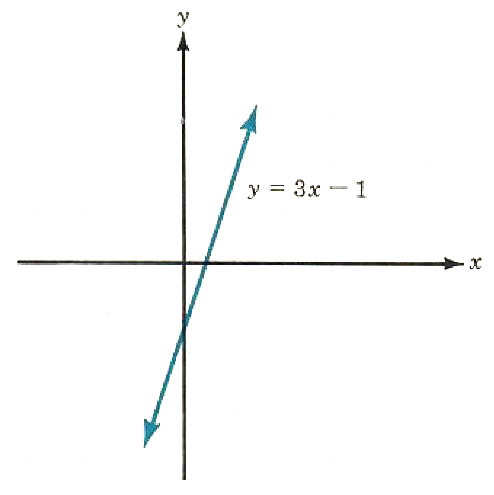
Figure 8.6
To calculate the slope, find any two points on the line, then find the rise and the run using those two points (see Figure 8.7a). (The ratio of rise
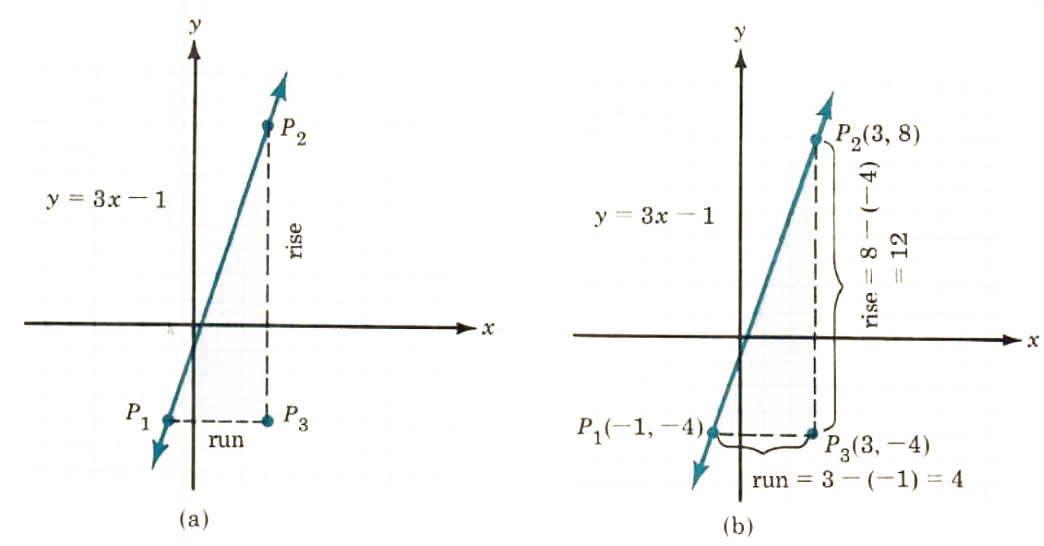
Figure 8.7
to run is the same for any two points on a line.) For example,
x=3 y=3(3)-1=9-1=8
x=-1 y=3(-1)-1=-3-1=-4
Now, using P_1(-1, -4) and P_2(3, 8), the coordinates of P_3 are (3, -4), as shown in Figure 8.7b. P_3 has the same x-coordinates as P_2 and the samey-coordinates as P_1.
(Note: The notation P_1 is read “P sub 1" and the 1 is called a subscript. Similarly, P_2 is read “P sub 2,” and P_3 is read “P sub 3.”)
For the line y=3x-1,
slope=(rise)/(run)=(8-(-4))/(3-(-1))
=12/4=3
Now find the slope of the line y=3x+2. Locate two points on the line and calculate the ratio, rise/run
For example,
x=0 y=3*0+2=0+2=2
x=1 y=3*1+2=3+2=5
Thus, P_1(0, 2), P_2(1, 5), and P_3(1, 2), are as shown in Figure 8.8.
Notice that the two lines y = 3x - 1 and y = 3x + 2 have the same slope, 3. (See Figure 8.9.) This means that the lines are parallel. All lines with the same slope are parallel. All the lines in Figure 8.9 have slope 3 and are parallel.
By using subscript notation, we can develop a formula for the slope
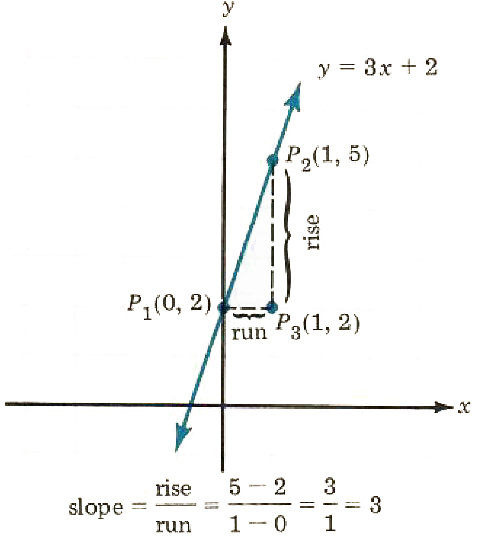
Figure 8.8
of any line. Let P_1(x_1,y_1) and P_2(x_2, y_2) be two points on a line. Then P_3(x_2, y_1) is at the right angle shown in Figure 8.10, and the slope can be calculated.
slope=(rise)/(run)=(y_2-y_1)/(x_2-x_1)
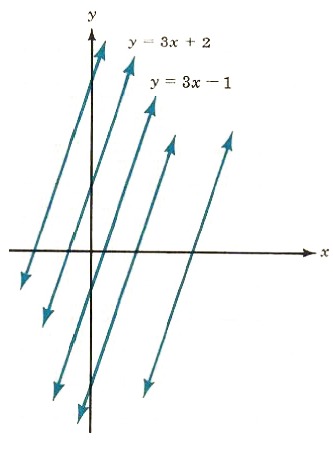
Figure 8.9
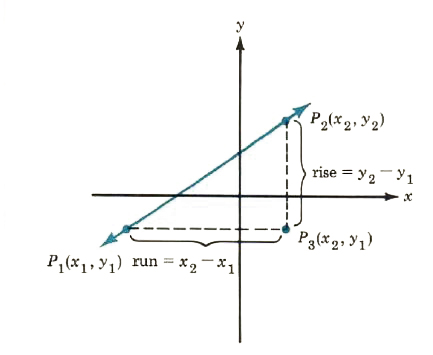
Figure 8.10
Examples
1. Using the formula for slope, find the slope of the line 2x + 3y = 6.
Let x_1=0
2.0+3y_1=6
3y_1=6
y_1=2
Let x_2=-3
2(-3)+3y^2=6
-6+3y_2=6
3y_2=12
y_2=4
(x_1,y_1)=(0,2) and x_2,y_2)=(-3,4)
slope=(y_2-y_1)/(x_2-x_1)=(4-2)/(-3-0)=2/(-3)=-(2/3)
2. Suppose that the order of the points in example 1 is changed. That is, (x_1,y_1)=(-3,4) and (x_2,y_2) = (0, 2). Will this make a difference in the slope?
slope=(y_2-y_1)/(x_2-x_1)=(2-4)/(0-(-3))=-2/(3)=-(2/3)
Changing the order of the points does not make a difference in the calculation of the slope. Both the numerator and denominator change sign, so the fraction has the same value. In example 1, 2/-3=-(2/3) and in example 2, -2/3=-(2/3) The important procedure is that the coordinates must be subtracted in the same order in both the numerator and the denominator.
In general,
slope=(y_2-y_1)/(x_2-x_1)=(y_1-y_2)/(x_1-x_2)
The negative slope for the line 2x + 3y = 6 means that the line slants (or slopes) downward to the right (see Figure 8.11). All lines with negative slopes slant downward to the right and all lines with positive slopes slant upward to the right.
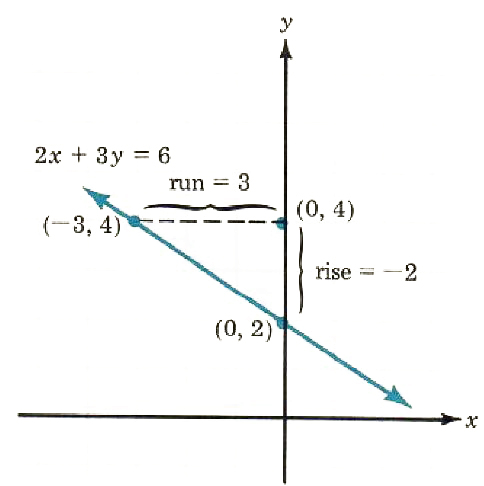slope=-2/3=-(2/3)
Figure 8.11
Example Graph the line with slope m=3/4 which passes through the point (4, 5). Start from the point (4, 5) and locate another point on the line using the slope as (rise)/(run)=3/4.
Four units to the right (run) and three units up (rise) from (4, 5) will give another point on the line. From (4, 5) you might have moved 4 units left and 3 units down, or 8 units right and then 6 units up. Just move so that the ratio of rise to run is 3 to 4 and you will locate a second point on the graph. (For a negative slope, move either to the right and then down or to the left and then up.)
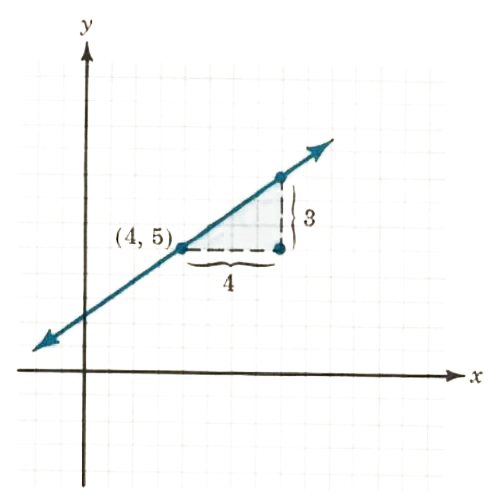
Solve the equation 2x+3y=6 for y.
2x+3y=6
3y=-2x+6
(3y)/3=(-2x+6)/3
y=(-2x)/3+6/3
y=-(2/3x)+2
Note that the coefficient of x,-(2/3), is the same as the slope of the line. Also, for lines previously discussed, y = 3x -1 and y = 3x + 2, the slope of each line was 3, which is the coefficient of x. If a linear equation is solved for y, will the coefficient of x always be the slope? This is an important question and the answer can be found in the following discussion.
Suppose that the equation is solved for y and y=mx+b. Let (x_1,y_1) and (x_2,y_2) be two points on the line. (x_1!=y_1) Then,
y_1=mx_1+b and y_2=mx_2+b
slope=(y_2-y_1)/(x_2-x_1)=((mx_2+b)-(mx_1+b))/(x_2-x_1)
=(mx_2+b-mx_1-b)/(x_2-x_1)=(mx_2-mx_1)/(x_2-x_1)
=
The slope is m, the coefficient of x, in the form y = mx + b
For the line y = mx + b, let x=0. Then y=m*0+b=b and y = b is the y-intercept. Since m is the slope and b is the y-intercept, we are led to the following definition.
y = mx + b is called the slope-intercept form for the equation of a line; m is the slope and b is the y-intercept.
Find the slope (m) and the y-intercept b of each of the following lines by rewriting the equation in the slope-intercept form, Then graph the line.
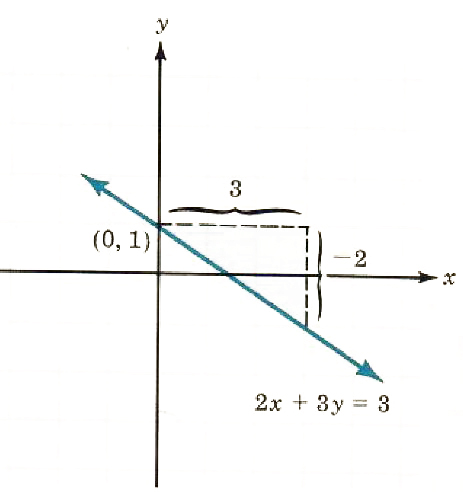
1. 2x+3y=3
3y=-2x+3
y=(-2x+3)/3
y=-(2/3x)+1
m=-(2/3)
y-intercept = 1.
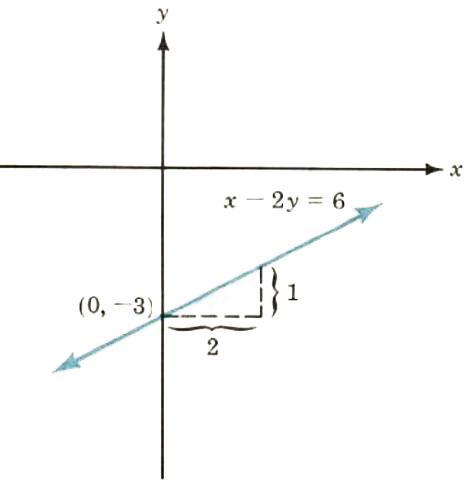
2. x-2y=6
x=6+2y
x-6=2y
(x-6)/2=y
1/2x-3=y
m=1/2 b=-3
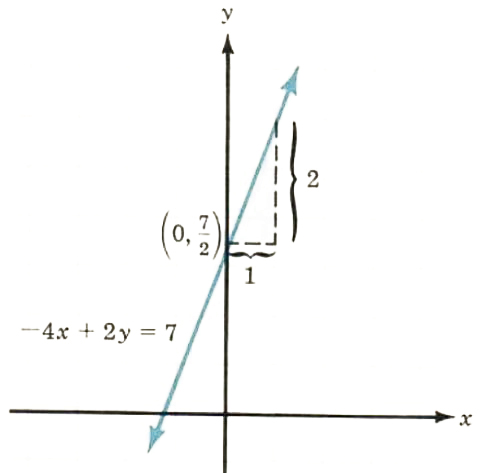
3. -4x+2y=7
2y=4x+7
y=(4x+7)/2
y=2x+7/2
m=2 b=7/2
If a line is to have a certain slope and pass through a particular point, the equation representing the line can be found as in the following illustration.
Suppose that the line is to have slope § and pass through the point (1, 5). If (x, y) is to represent a point on the line, then the slope calculated using (1, 5) and (x, y) must be 2/3. That is,
(y-5)/(x-1)=2/3
In another form,
y-5=2/3(x-1)
More generally, a line with slope m that passes through a fixed point (x_1,y_1) can be represented in the form
y-y_1=m(x-x_1)
y-y_1=m(x-x_1) is called the point-slope form for the equation of a
line; m is the slope and (x_1,y_1) is the fixed point.
Examples
1. Find the equation of the line that has slope m=3/4 and passes through the point (4,5).
y-y_1=m(x-x_1)
y-5=3/4(x-4) (the equation in the point-slope form)
or y-5=3/4x-3
y=3/4x+2 (the equation in the slope-intercept form)
or 4y=3x+8
-3x+4y=8 (the equation in the standard form, Ax+By=C)
2. Find the equation of the line passing through the two points (- 1, -3) and (5, -2).
m=(y_2-y_1)/(x_2-x_1)=(-2-(-3))/(5-(-1))=(-2+3)/(5+1)=1/6Find m using the formula for slope .
Using the point-slope form (either point (-1, -3 or (5, -2) will give the same result)
y-(-2)=1/6(x-5)
y+2=1/6(x-5) (the equation in the point-slope form)
or y+2=1/6x-5/6
y=1/6x-17/6 (the equation in the slope-intercept form)
or 6y=x-17
17=x-6y (the equation in the standard form, Ax+By=C)
Any of the three basic forms for the equation of a line is acceptable. In any case, if an answer is given in a form different from yours, you should be able to recognize the equations as equivalent.
Let's see how our math solver generates graphs of straight lines and see the various slope of lines. Click on "Solve Similar" button to see more examples.
8.4 Horizontal and Vertical Lines
Consider the equation y = 3. If x = 5, what is y? If x = -2, what is y? If x=0, what is y? In each case, y = 3. The points (5, 3), (-2, 3), and (0,3) all satisfy the condition y = 3. x can have any value, but y must be x. To emphasize this fact, the equation y = 3 could be written 0x + y = 3 or y = 0x + 3. The graph of the equation y = 3 is a horizontal line, and each y-coordinate is 3. (See Figure 8.12.)
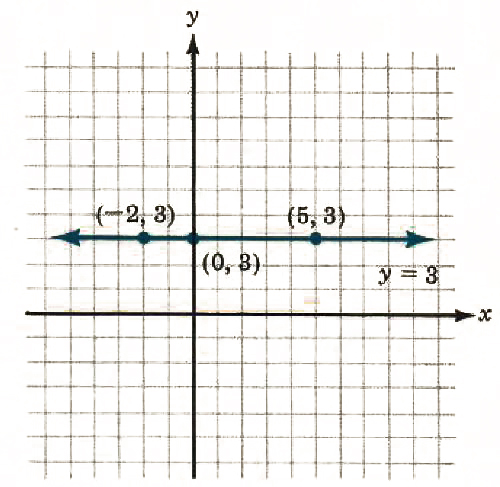
Figure 8.12
What is the slope of the line y = 3? By writing the equation in the form y = 0x + 3, the slope is 0. Also, by the formula for slope, using (-2, 3) and (5, 3), the slope is indeed 0:
slope = m=(y_2-y_1)/(x_2-x_1)=(3-3)/(5-(2))=0/7=0
What are the graphs of the equations y = -2 and y = 3/2? Both are horizontal lines with slope 0. In fact, any equation of the form y = b (or y = 0x + b) is a horizontal line with slope 0 (see Figure 8.13). Now consider the equation x = 2. If y = 4, what is x? If y = -3 what is x? If y = 0, what is x? In each case, x = 2. The points (2,4), (2, -3), and (2, 0) all satisfy the condition x = 2. y can have any value, but x must be 2 .We can write x = 2 in the form 0y +x = 2 or x =0y + 2 The graph of the equation x = 2 is a vertical line, and each x-coordinate is 2 (see Figure 8.14).
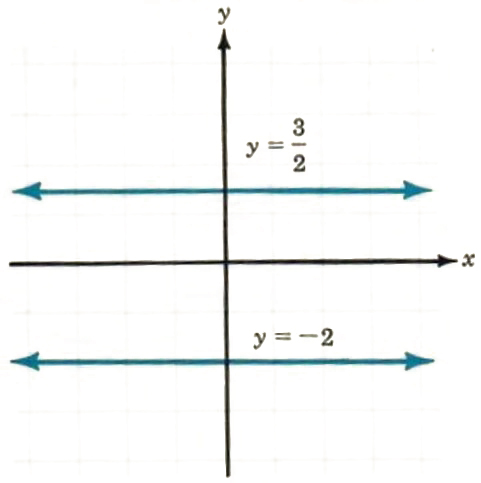
What is the slope of the line x = 2 ? To answer this question, let us use the slope formula and the two points (2, 4) and (2, -3):
slope = m=(y_2-y_1)/(x_2-x_1)=(4-(-3))/(2-2)=7/0 undefined
The slope is undefined because 0 cannot be a denominator. This is true for any vertical line. The graphs of equations of the form x = a are vertical lines with no slope (or slope undefined). Note very carefully the distinction that horizontal lines ((y = b)) have 0 slope and vertical lines (x=a)) have no slope. Both the equations for horizontal lines ((y = b)) and the equations for vertical lines (x=a)) are special cases of the general linear equation in standard form, Ax + By = C, discussed in Section 8.2.
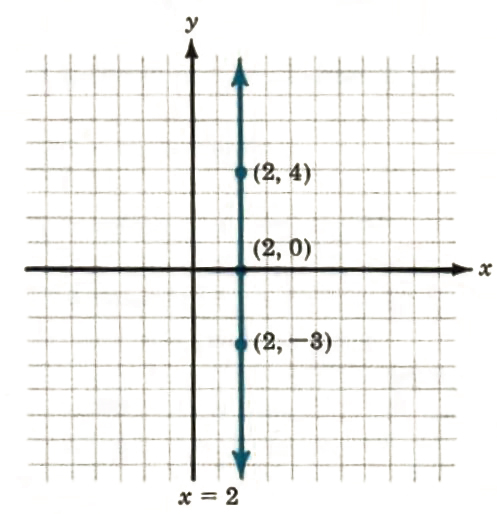
Figure 8.14
Examples
For each of the following linear equations, find the slope of the line, if it exists, and graph the line.
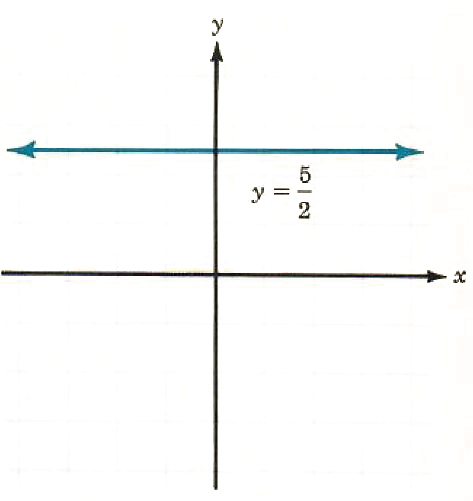
1. 2y=5
y=5/2
m=0
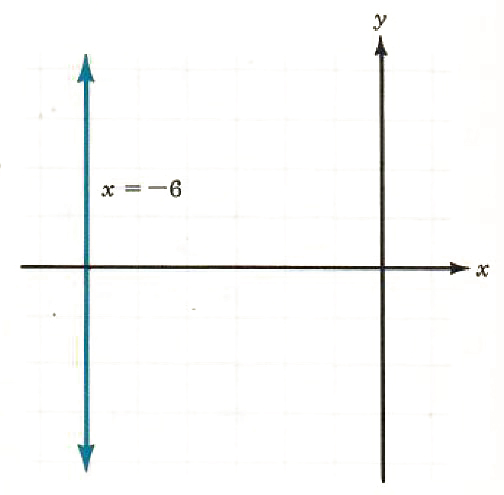
2. x+6=0
x=-6
no slope
3. x+y=0
y=-x
m=-1
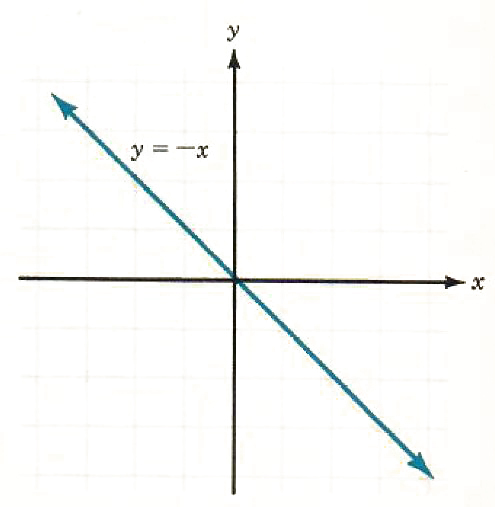
8.5 Distance Between Two Points
What is the distance between the two points P_1(2, 3) and P_2(6, 3)? What is the distance between the points P_3(-1, -4) and P_4(-1, 1) ? (See Figure 8.15.)
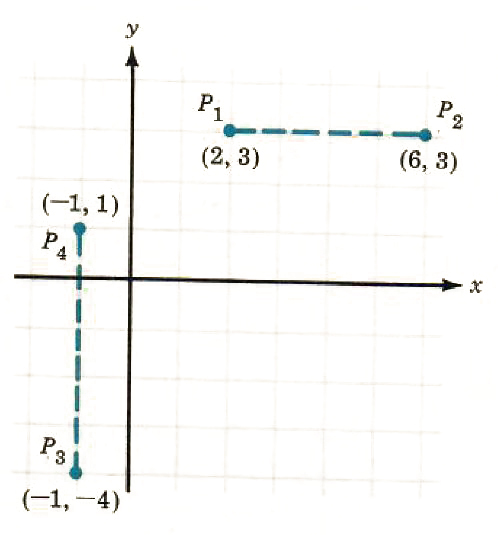
Figure 8.15
Did you find
distance ( P_1 to P_2)=6-2=4?
This is correct since P_1 and P_2 lie on a horizontal line and have the same y -coordinate. Did you find
distance (P_3 to P_4)=1-(-4)=5?
This is correct since P_3 and P_4 lie on a vertical line and have the same x-coordinate.
For the distance from P_1 to P_2, why not take
distance (P_1 to P_2) = 2-6=-4?
The reason is that the term distance is taken to mean a positive number, How can a positive number be guaranteed after we subtract the coordinates? The answer is to take the absolute value of the difference of the coordinates. The distance between two points is represented by d.
For P_1(x_1,y_1) and P_2(x_2,y_1) on a horizontal line,
For P_1(x_1,y_1)and P_2(x_1,y_2)on a vertical line,
Examples
1. Find the distance, d, between the two points (5, 7) and (-3, 7). Since the points are on a horizontal line (they have the same y-coordinate),
or 
2. Find the distance, d, between the two points (2, 8) and 2,-(1/2). Since the points are on a vertical line (they have the same x:coordinate),
or 
What if the points do not lie on a vertical line or on a horizontal line? Indeed, this is the more general case. We need the Pythagorean Theorem. The Pythagorean Theorem, stated here, will be discussed in greater detail in Section 10.6.
Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the two sides.
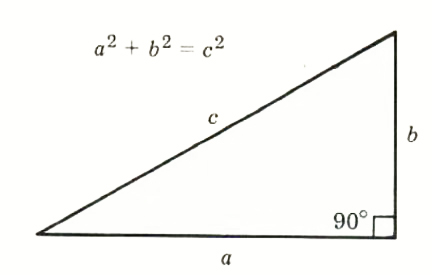
To find the distance between the two points P_1( - 1, 2) and P_2(5, 4), apply the Pythagorean Theorem and calculate the length of the hypotenuse as shown in Figure 8.16.
We could write directly d = root(a^2 + b^2). Carrying this idea one step farther, we can write a formula for d involving the coordinates of two general points P_1(x_1,y_1) and P_2(x_2,y_2).
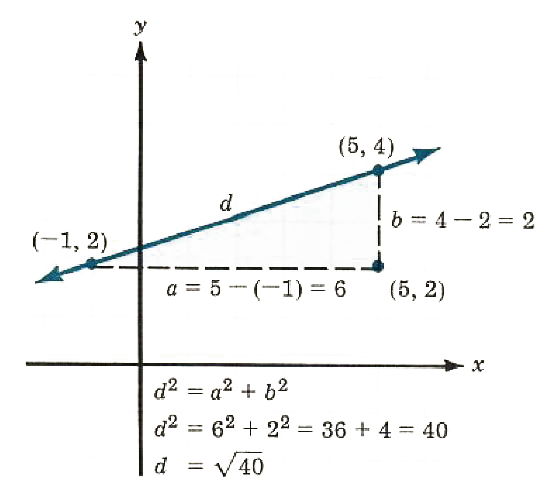
Figure 8.16
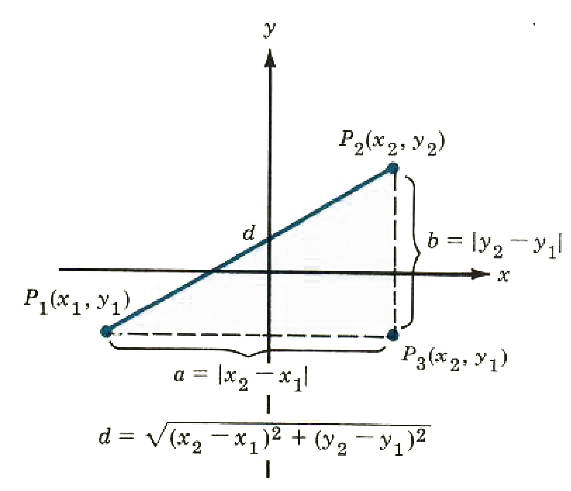
Do we need |x_2-x_1| and |y_2 - y_1| in the formula? Evidently not, but why not? The answer is that even though x_2 - x_1 and y_2 - y_1 might be negative, both are being squared, so neither of the terms (x_2 - x_1)^2 or (y_2 - y_1)^2 will ever be negative‘ In the actual calculation of d, be sure to add the squares before taking the square root.
Examples
1. Find the distance between the two points (3, 4) and (-2, 7).
d=root((3-(-2))^2+(4-7)^2)
=root(5^2+(-3)^2)
=root(25-9)
=root(34)
2. Find the distance between the two points (1/2,2/3) and (3/4,5/3).
d=root((1/2-3/4)^2+(2/3-5/3)^2)
=root((-1/4)^2+(-3/3)^2)
=root(1/16+1)
=root(1/16+16/16)
=root(17/16)
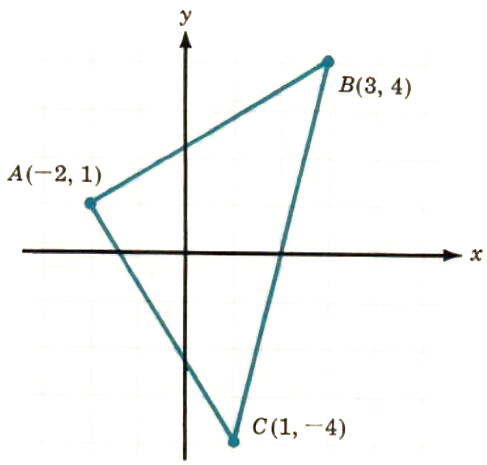
3. Show that the triangle determined by the points A(-2, 1), B(3,4), and C(1, -4) is an isosceles triangle. An isosceles triangle has two equal sides.
Solution:
The length of the line segment 
is the distance between the points A and B. We denote this distance by 
. Thus, to show that the triangle ABC is isosceles, we need to show that = 
or that = 
. If neither of these relationships is true, then the triangle does not have two equal sides and is not isosceles.
= root((-2-3)^2+(1-4)^2) = root((-5)^2+(-3)^2)
= root(25+9)=root(34)
= root((-2-1)^2+[1-(-4)]^2) = root((-3)^2+(5)^2)
=root(9+25)=root(34)
Since = , the triangle is isosceles
