Example: x-y>2,y>x^2
To see your tutorial, please scroll down
Functions of One variables and more than one variable
7.7 Functions of One Variable
A function of one variable is a rule of correspondence that assigns to each number in one set a unique number in another possibly different set. The first set is called the domain of the function and the second set is called the range. If f denotes the function and a denotes a number in the domain, then f(a) denotes the number in the range that f assigns to a. The number f(a) is called the value of f at a. If x is a variable over the domain of f, we say that f is a function of the variable x or simply a function of x.
Many functions have their rule of correspondence defined by algebraic expressions. For example, the equation
f(x)=2x+3
defines a function f. To use this equation to find the number that f assigns to 4, we simply replace each occurrence of x by 4. We have
f(4)=2(4)+3
=11
and thus the value of f at 4 is 11.
When a function f is defined by an equation its domain is under-stood to be the set of all real numbers for which the right-hand side of the equation is defined. For the above function f, since 2x+3 is defined for all real numbers x, the domain off is the set of all real numbers.
Example 1.
Let g and h be functions defined by g(x)=(x+1)/(x-1) and h(x)=root(x+2) find (a)g(0),(b)g(1/2),(c)h(-1) and (d)h(1/4).
(a) g(0)=(0+1)/(0-1)
=-1
(b) g(1/2)=(1/2+1)/(1/2-1)
=(3/2)/(-1/2)
=-3
(c) h(-1)=root((-1)+2)
=root(1)
=1
(d) h(1/4)=root((1/4)+2)
=root(9/4)
=3/2
Example 2.
Find the domains of the functions g and h defined in Example 1. Since (x+l)/(x-1) is defined for all x except x=1, the domain of g is the set of all real numbers except 1. The expression root(x+2) is defined only when x+2 is non-negative. We see that x+2 is non- negative if and only if x is greater than or equal to -2. Thus the domain of h is the set of all real numbers greater than or equal to -2.
By the graph of a function f we mean the graph of the equation
y=f(x)
Thus the graph of the function f, which is defined by f(x)=2x+3, is the graph of the equation y=2x+3. This graph is the straight line with slope 2 and Y intercept 3. In order to graph f we find the points on the graph whose first coordinates are 0 and 2.
At x=0,
y=f(0)
=2(0)+3
=3
At x=2,
y=f(2)
=2(2)+3
=7
Thus, these two points are
(0,f(0))=(0,3)
(2,f(2))=(2,7)
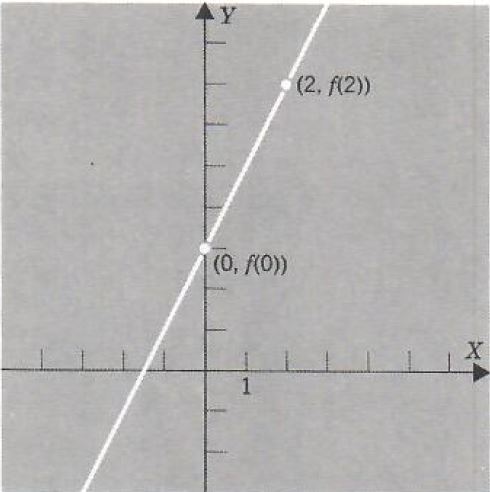
Note that at x=0 the directed distance from the X axis to the graph offis f(0)=3, while at x=2 it is f(2)=7. In general, if f is any function, then at x=a the directed distance from the X axis to the graph of f is just f(a). See Figure 9.
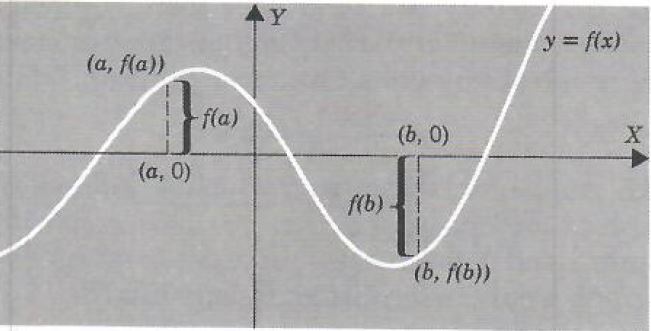
FIGURE 3.
Example 2.
Graph the function h defined by h(x)=x^2-4. Indicate the distances h(-3) and h(1) on the graph.
The graph of h is the graph of the equation
y=x^2-4
This is a parabola with vertex (0,-4), axis of symmetry the Y-axis, and opening upward.
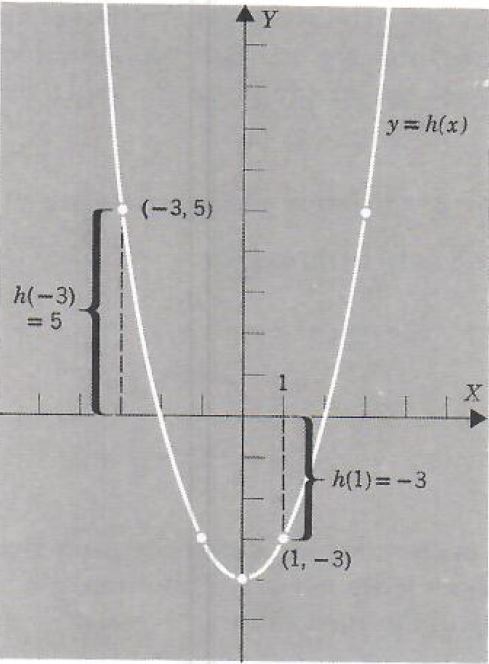
| x | y=h(x) |
| -3 | 5 |
| -1 | -3 |
| -2 | 0 |
| 0 | -4 |
| 1 | -3 |
| 2 | 0 |
| 3 | 5 |
Let's see how our math solver generates graphs for this and similar functions. Please click on "Solve Similar" to see more examples.
A Function f can also be defined by a graph rather than an equation. Since the points on the graph are exactly those with coordinates (a,f(a)), we can find f(a) by measuring the directed distance from the point (a,0) on the X axis to the point (a,f(a)) on the graph.
Example 4.
Find f(3) where the function f is given by the graph below.
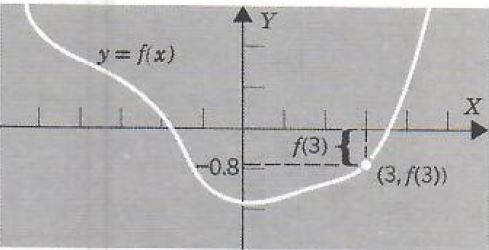
To estimate f(3) we measure the directed distance from the point
(3,0) to the point (3,f(3)). This can be done by drawing the horizontal line from (3,f(3)) to the Y axis and estimating the Y coordinate of the point of intersection. We see that f(3) is approximately -0.8. We write
f(3)≈-0.8
Where "-0.8" means “approximately equal to."
A function is sometimes defined by an equation in two variables
If we have an equation in x and y that determines at most one value of y for each value of x, then we say that the equation defines y as a function of x. Of course, not all equations in x and y define y as a function of x.
Example 5.
Does 2x+4y-3=0 define y as a function of x?
We solve this equation for y in terms of x.
2x+4y-3=0
4y=-2x+3
y=-1/2x+3/4
It is clear that for each value of x the equation does determine a unique value of y, hence it defines y as a function of x.
Consider the graph of this equation:
2x+4y-3=0
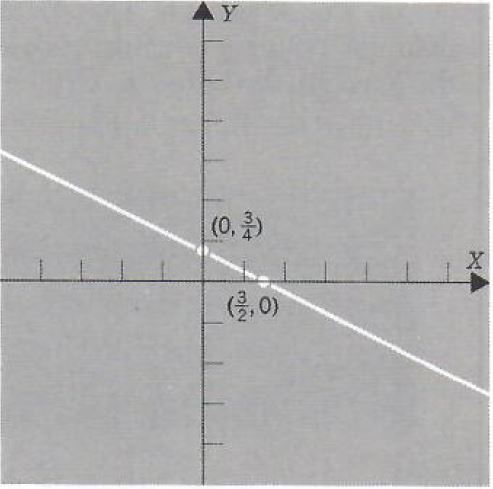
Interpreting geometrically the condition that each x determines a unique y, we see that an equation defines y as a function of x if for each value of x the vertical line on (x,0) intersects the graph at most once. The above graph certainly has this property.
Example 6.
Does x-1-y^2=0 determine y as a function of x? Discuss algebraically and geometrically.
Solve the equation for yy.
x-1-y^2=0
y^2=x-1
y=+-root(x-1)
We see that for certain values of x, the equation determines two values of y, for example, for x=2 both y=1 and y=-1 are solutions. Thus this equation does not define y as a function of x. Now graph the equation.
x-1-y^2=0
x-1=y^2
We see that the graph is a parabola with vertex (1, 0), axis of symmetry the X axis, and opening to the right.
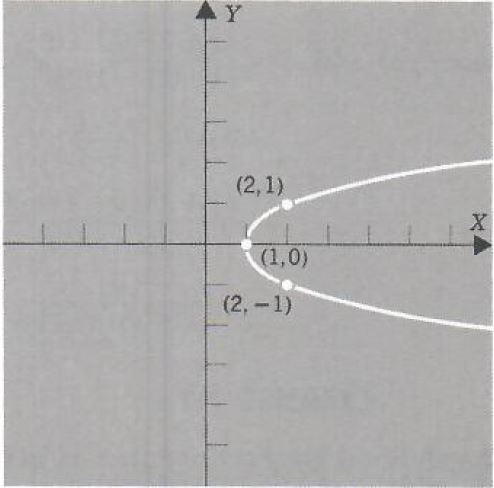
| x | y |
| 1 | 0 |
| 2 | +-1 |
Each vertical line on (x, 0), where x is greater than 1, intersects the graph twice. This tells us geometrically that this equation does not define y as a function of x.
Many situations arise where functions must be evaluated at various expressions. We consider some examples.
Example 7.
Let h be defined by h(x)=(x+1)/(x-1). Compute (a)h(1+t),(b)h(1/r),(c)h(x^2), and (d) h(x+2)-h(x).
(a) h(1+t)=((1+t)+1)/((1+t)-1)=(t+2)/t
(b) h(1/r)=((1/r)+1)/((1/r)-1)=((1+r)/r)/((1-r)/r)=(1+r)/(1-r)
(c) h(x^2)=((x^2)+1)/((x^2)-1)=(x^2+1)/(x^2-1)
(d) h(x+2)-h(x)=((x+2)+1)/((x+2)-1)-(x+1)/(x-1)
=(x+3)/(x+1)-(x+1)/(x-1)
=((x+3)(x-1)-(x+1)^2)/((x+1)(x-1))
=-(4/((x+1)(x-1))
7.8 Functions of More Than One Variable
Sometimes it is necessary to use a function whose domain is a set of pairs of numbers. Let f denote such a function and let (x, y) be a pair of variables over the domain of f. Then f(x,y) denotes the value off at the pair (x, y), and f is a function of the two variables x and y.
Example 1.
Let f be defined by the equation f(x,y)=x+y+xy. Evaluate f when (x,y) has the following values: (a)(1,2), (b)(-3,1/2), (c)(a+1,b-3).
(a) f(1,2)=1+2+(1)(2)=5
(b) f(-3,1/2)=-3+1/2+(-3)(1/2)=-4
(c) f(a+1,b-3)
=(a+1)+(b-3)+(a+1)(b-3)
=-2a+2b+ab-5
Example 2.
For g(x,y) defined by g(x,y)=x^2+y-3, find each of the following : (a) g(1+h,-2+k)-g(1,-2), (b) g(x+h,y+k)-g(x,y), (c) g(1/x,y) and (d) g(x^2,x+2).
(a) g(1+h,-2+k)-g(1,-2)
=((1+h)^2+(-2+k)-3)-(1^2+(-2)-3)
=1+2h+h^2-2+k-3-1+2+3
=h^2+2hx+k
(b) g(x+h,y+k)-g(x,y)
=((x+h)^2+(y+k)-3)-(x^2+y-3)
=x^2+2hx+h^2+y+k-3-x^2-y+3
=h^2+2hx+k
(c) g(1/x,y)=(1/x)^2+y-3=1/x^2+y-3
(d) g(x^2,x+2)=(x^2)^2+(x+2)-3=x^4+x-1
For functions of three or more variables the notation and computations are similar.
Example 3.
Let F be the function of x,y, and z defined by F(x,y,z)=(x^2+y^2+z^2-2x+4y-6z). Compute F at (a) (1,0,1) and (b) (x+1,y-2,z+3).
(a) F(1,0,1)=1^2+0^2+1^2-2(1)+4(0)-6(1)=-6
(b) F(x+1,y-2,z+3)
=(x+1)^2+(y-2)^2+(z+3)^2-2(x+1)+4(y-2)-6(z+3)
=x^2+2x+1+y^2-4y+4+z^2+6z+9-2x-2+4y-8-6z-18
=x^2+y^2+z^2-14
Functions of one or more variables arise when we solve an equation in two or more variables for one variable in terms of the others. The resulting equation expresses the one variable as a function of the other variables.
Example 4.
Consider xy+x-yz=z Express y as a function of x and z.
xy+x-yz=z
xy-yz+x=z
(x-z)y=z-x
y=(z-x)/(x-z)
Example 5.
Express the height of a cylinder as a function of its volume and the radius of its base.
From geometry we know that if V is the volume, r is the radius, and h is the height, then
V=PIr^2h
Solving this equation for h we obtain
Thus h=h(r,V), where h(r,V)=V/(PIr^2)