IMPLICIT DIFFERENTIATION
The equation y = x2 + 1 explicitly defines y as a function of x, and
we show this by writing y = f (x) = x2 + 1. If we write the equation
y = x2 + 1 in the form y - x2 - 1 = 0, then we say that y
is implicitly a function of x. In this case we can find out what that function
is explicitly simply by solving for y. Sometimes, however, we must deal with
equations relating y to x that are so complicated that it is difficult or even
impossible to solve for y in terms of x. (For example, try to solve for yin the
equation yy + xy = 10.) If an equation implicitly defines y as a
function of x, there is a way to find dy/dx without first explicitly finding y
as a function of x, called implicit differentiation.
We will use the equation y - x2 - 1 = 0 to illustrate this technique.
Instead of explicitly solving for y, assume that it would be possible to solve
for y in terms of x; call the resulting function y(x) for simplicity. The
equation can now be written as

Differentiating both sides with respect to x by means of the sum and power
rules, we obtain
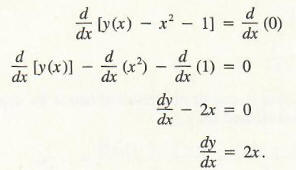
This same result would be obtained by solving for y so that y = x2
+ 1, from which dy/dx = 2x. In this example it is easier to first solve for y
and then differentiate, but this will not always be the case.
Example 1
Find the slope of the tangent line to the graph of the equation xy - x = 1 at
that point on the graph whose first coordinate is 1 (that is, corresponding to x
= 1).
Solution
We must find dy/dx at x = 1. Assume y is a function of x, y = y(x). The relation now is xy(x) - x = 1.
Hence,
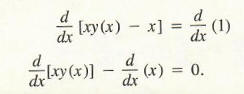
and by the extended power rule,

Substituting these results into Formula (2), we obtain
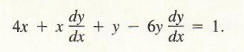
We solve this equation for dy/dx:

Be careful! When applying Formula (3), keep in mind that the only values
of x and y that can be substituted into the right-hand side of Formula (3) are
those values that satisfy the original condition 2x2 + xy - 3y2
= x. For instance, we might substitute x = 1, y = 4 to obtain (dy/dx) = (1 - 4 -
2)/(1 - 12) = 5/1; however, (1, 2) is not a point on the graph of 2x2
+ xy - 3y2 = x, so the calculation of dy/dx at this point is totally
meaningless.
The equation in Example 2 can be written as - 3y2 + xy + (2x2
- x) = 0 and hence is a quadratic equation in y (an equation of the form Ay2
+ By + C = o where A = -3, B = x and C = 2x2 - x). Hence, we could
use the quadratic formula to solve this equation for y in terms of x, obtaining

Though we are able to find y explicitly in terms of x , the resulting
expression is fairly complex, and it still might be best to find dy/dx
implicitly as in Example 2.
Example 3 Find dy/dx if y4 + xy = 10.
Solving for y in terms of x is difficult if not impossible in this problem.
However, by implicit differentiation, we obtain

The following example illustrates how implicit functions can be used to
justify the fact that dxn /dx = nxn-1 i is valid when n is
a rational number.
Example 4 Let f(x) = x2/3. Use implicit differentiation to
show that

Since f(x) = x2/3 , we obtain, by cubing,
[f(x)]3 = x2.
Differentiate with respect to x.

Hence,
